|
|
The chain rule
applications |
Derivative of
parametric functions, parametric derivatives |
|
Derivative of
parametric functions example
|
|
Derivative
of vector-valued functions |
|
|
|
|
|
|
| Derivative of
parametric functions, parametric derivatives |
| When
Cartesian coordinates of a curve is represented as
functions of the same variable (usually written
t),
they are
called the parametric equations. |
| Thus,
parametric equations in the xy-plane |
| x
= x (t)
and y
= y (t)
or x
= f (t)
and y
= g (t), |
| denote
the x
and y
coordinate of the graph of a curve in the plane. |
| Assume
that f
and g
are differentiable and f
'(t) is not
0 then, given parametric curve can be
expressed as y
= y (x) and this
function is differentiable at x,
that is |
|
x
= f (t)
or
t = f -1(x), |
|
by plugging
into y
= g (t)
obtained is y
= g [f -1(x)]. |
| Therefore,
we use the chain rule and the derivative of the inverse function to find
the derivative of the parametric
functions, |
 |
|
|
|
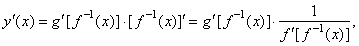| Derivative of
parametric functions example
|
|
Example:
Write
equation of the line tangent to the curve x
= t
+
1 and
y
=
-
t2
+
4
at the point t
= 1.
|
| Solution:
The equation x
=
t + 1
solve for t
and plug into y
=
- t2 + 4,
thus |
| t
=
x
- 1
=> y
=
- t2 + 4,
y
=
- (x
- 1)2 + 4 |
| i.e., y
-
4
=
- (x
- 1)2
or y
=
- x2 + 2x + 3 translated parabola with the vertex V(x0,
y0),
so V(1,
4). |
| When
plotting points of a parametric curve by increasing t, the
graph of the function is traced
out in the direction of motion. |
 |
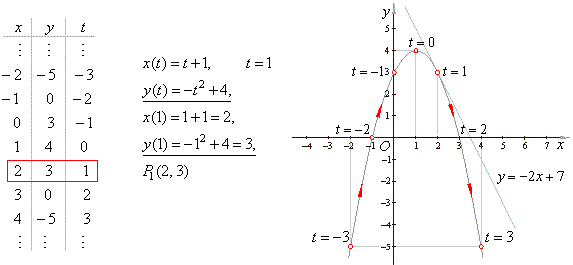| The
derivative of the given parametric equations at t
= 1 is the slope of the tangent
line, |
 |
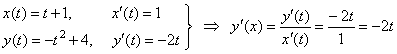| since
t
=
x
- 1
then m
=
y' (x)
=
-
2(x
- 1)
= -
2(2
- 1)
=
-
2,
m
=
-
2.
|
| Therefore,
the equation of the line tangent to the given parametric curve at t
= 1 or the point P1(2,
3) is |
|
y
- y1
= m(x
- x1),
y
- 3
= -
2(x
- 2) =>
y
= -
2x
+ 7. |
|
| Derivative
of vector-valued functions |
| If
the radius vector r
of a point in a plane depends on a parameter t,
say t
represents time, so that its magnitude
and direction change continuously while t
changes, then its arrow sweeping out a curve. |
| Let
r (t)
denotes its value at the moment t
and r (t
+ h)
represents its value at t
+ h,
and P
and P1
are the corresponding
points of the curve, as is shown in the figure below. |
