|
|
The chain rule
applications |
 Derivatives of the hyperbolic functions
Derivatives of the hyperbolic functions |
|
Derivatives of inverse hyperbolic functions |
 Derivative of
the inverse function
Derivative of
the inverse function |
|
Derivatives of the inverse trigonometric functions |
|
|
|
|
|
|
|
Derivatives of the hyperbolic functions |
| We
use the derivative of the exponential function and the chain rule to
determine the derivative of the hyperbolic
sine and the hyperbolic cosine functions. |
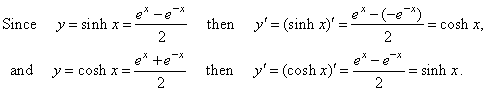 |
| We
find derivative of the
hyperbolic tangent and the hyperbolic cotangent functions applying
the quotient rule. |
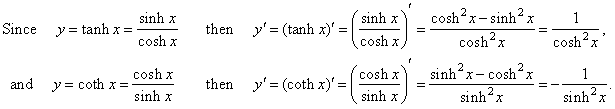 |
| Therefore,
derivatives of the hyperbolic functions are |
|
|
|
|
Derivatives of inverse hyperbolic functions |
| We
use the derivative of the logarithmic function and the chain rule to
find the derivative of inverse hyperbolic functions. |
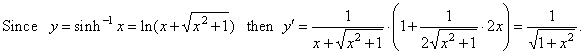 |
| We
use the same method to find
derivatives of other inverse hyperbolic functions,
thus |
|
|
|
|
Derivative of the inverse function |
| If
given a function y =
f (x) the derivative of
which y' (x)
is
not 0
then, the derivative of the
inverse function x
= f -1
(y) is |
|
|
|
|
Example:
Find
the derivative x'(y)
if the given function f
(x)
= x
+
ln x.
|
| Solution: |
 |
|
|
|
Derivative of the inverse trigonometric functions |
| 1)
The derivative of the inverse of the sine function y =
sin -1x,
| x | < 1
and -p/2
< y < p/2
if x = sin y,
then |
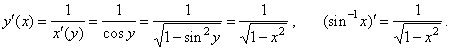 |
| 2)
The derivative of the inverse of the cosine function y
= cos -1x =
p/2
-
sin
-1x,
| x | < 1,
0
< y < p |
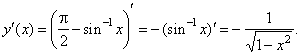 |
| 3)
The derivative of the
inverse of the tangent function y =
tan -1x,
-
oo
< x < oo
and
-p/2
< y < p/2
if x = tan y,
then |
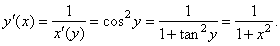 |
| 4)
The derivative of the
inverse of the cotangent function y =
cot -1x
= p/2
-
tan -1x, |
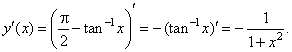 |
| 5)
The derivative of the
inverse of the secant function y =
sec -1x
= cos -1(1/x), |
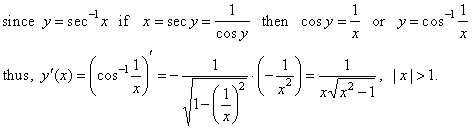 |
| 6)
The derivative of the
inverse of the cosecant function y =
csc -1x
= sin -1(1/x), |
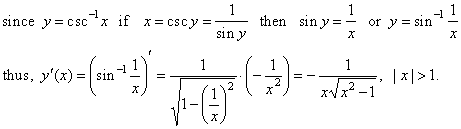 |
| Therefore,
derivatives of the inverse trigonometric functions are |
|
|
|