|
|
Applications of the derivative |
 Angle
between two curves
Angle
between two curves |
|
Angle
between two curves, examples |
|
|
|
|
|
|
| Angle
between two curves |
| Angle between two curves is the angle subtended by tangent lines at the point where the curves
intersect. |
| If curves
f1(x)
and f2(x)
intercept at P(x0,
y0)
then |
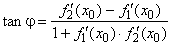 |
| as
shows the right figure. |
| |
|
 |
|
|
| Angle
between two curves, examples |
| Example: Find
the angle between cubic y
= -
x3 + 6x2 -
14x + 14 and quadratic y
= -
x2 + 6x -
6 polynomial. |
| Solution: To
find the point where the curves intersect we should solve their
equations as the system of two equations
in two unknowns simultaneously. Therefore, |
| -
x3 + 6x2 -
1
4x + 14
= -
x2 + 6x -
6
or x3
-
7x2 + 20x -
20 = 0
|
| the
root of the cubic equation we calculate using the formula |
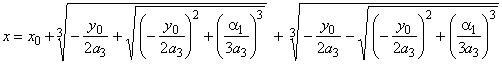 |
| where, |
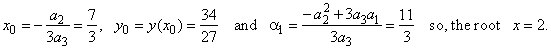 |
|
| Then, we
calculate the slopes of the tangents drown to the given cubic and the
quadratic polynomial by evaluating
their derivatives at x
= 2. Thus, |
| taking
f2(x)
= -
x3 + 6x2 -
14x + 14
so that f
'2(x)
= -
3x2 + 12x -
14
then f '2(2)
= -
2 |
|
and f1(x)
= -
x2 + 6x -
6
so that f '1(x)
= -
2x + 6
then f '1(2)
= 2. |
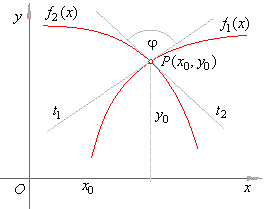
| Finally
we plug the slopes of tangents into the formula to find the angle
between given curves, as shows the
figure below. |
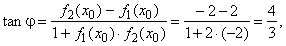 |
 |
| We
sketch the graphs of the quadratic and the cubic
by calculating coordinates of translations x0
and
y0,
as they are at the same time the coordinates
of the maximum and the point of inflection
respectively, thus |
| (x0)2
= xmax
= -
a1/(2a2) = 3,
y0
= f1(x0)
= 3, |
| (x0)3
= xinfl
= -
a2/(3a3) = 2,
y0
= f2(x0)
= 2. |
|
 |
|
|
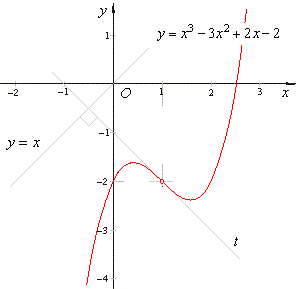
| Example: At
which point of the cubic y
= x3
-
3x2 + 2x -
2 is its tangent perpendicular to the
line y
= x. |
| Solution: Since
the slopes of perpendicular lines are negative reciprocals of each other
then, the slope of the
tangent to the cubic has to be
f ' (x)
= -1
to be perpendicular to the given line whose slope m
= 1. |
| Therefore, |
| f '
(x)
= 3x2 -
6x + 2,
we set f '
(x)
= -1
or 3x2
-
6x + 2
= -1
that gives x
= 1 |
|
the abscissa of the tangency point. Then, plug x
= 1 into the given cubic to calculate
its ordinate, |
| y
= x3
-
3x2 + 2x -
2,
y (1)
= -
2
so the tangency point I(1,
-2). |
| We
sketch the graph of the cubic
by calculating coordinates of translations x0
and
y0, |
| x0
= xinfl
= -
a2/(3a3) = 1,
y0
= f(x0)
= - 2 |
| what
coincide with the coordinates
of the point of
inflection I(1,
-2). |
| By
plugging x0
and
y0,
with changed signs, into the given
cubic, |
| y
- 2
= (x + 1)3
-
3(x +
1)2 + 2(x +
1) -
2 |
| we
get its source form |
| fs
(x)
= x3 -
x
or fs
(x)
= a3x3
+ a1x |
|
 |
|
| where
a1
= -
(a2)2 /(3a3)
+ a1,
a1
=
-1
and a1
= tan at,
as shows the figure above. |
|