|
| Integral
calculus |
|
|
|
|
The
definite integral |
 The area between the graph
of a function and the x-axis over a closed interval
The area between the graph
of a function and the x-axis over a closed interval
|
|
The upper sum and the lower sum |
 The definition of the definite integral
The definition of the definite integral |
|
|
|
|
|
|
|
| The area between the graph
of a function and the x-axis over a closed interval |
| The
problem of finding the area enclosed by the graph of a function and the x-axis
over a closed interval is solved
by use of the quadrature. The quadrature is the method of the calculation of
planar areas that consists of
the
construction of a square with the same area as a given figure or
surface. |
| Let
y = f (x)
be a continuous positive function defined on the closed interval [a,
b]. |
| Define
the area A
of a region of the coordinate plane bounded above by the graph
of f, below by the interval
[a, b]
on the x-axis,
and bounded to the left by the vertical line x
= a and on the right by the
vertical line x = b. |
|
|
The upper sum and the lower sum |
| Divide
the given interval [a,
b] into n
subintervals by a finite sequence of points such that |
| a
= x0
< x1 < x2 < . . . < xn
-
1 < xn
= b. |
| The
obtained subintervals are [a,
x1], [x1,
x2],
. . . , [xi
-
1, xi],
. . . , [xn
-
1, b]
|
| of
lengths Dx1,
Dx2,
. . . , Dxi
,
. . . ,
Dxn
where, Dxi
= xi -
xi
-
1
and ( i = 1, 2 , . . . , n ). |
| Since,
by the assumption f
is continuous on [a,
b]
then there exist the highest value M and
the lowest value m
of the function inside the interval [a,
b]
and similarly, inside the subinterval Dx1
it will have some highest value M1
and a lowest m1,
in Dx2
values M2
and m2,
. . . and in Dxn
a function values Mn
and mn. |
| Such
that always |
| mi
< Mi,
and
Mi
< M
as mi
> m |
|
( i = 1, 2 , . . . , n ),
because the highest value in a subinterval
cannot exceed the highest value of the function in the whole interval [a,
b],
as the lowest value in
a
subinterval cannot be lower than that in the whole interval, as is shown
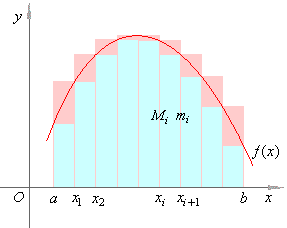
in the right figure. |
| Now
let write |
|
S
= M1
Dx1
+ M2
Dx2
+
·
· ·
+
Mn
Dxn |
|
 |
|
|
and s
= m1
Dx1
+ m2
Dx2
+
·
· ·
+
mn
Dxn,
where
S
represents the sum of areas of the circumscribed rectangles, each base
of witch is one of the subintervals Dxi
in the sequence, with height of the highest function value Mi
in that subinterval. Therefore, S
denotes the upper sum of f
over the interval [a,
b]. |
| While,
the sum s
denotes the lower sum of areas of the
inscribed rectangles with the same bases and with heights
that equal the lowest function value mi
in each subinterval, as shows the figure above. |
| Since
mi
< Mi
( i = 1, 2 , . . . , n ),
then s
< S |
| and
since, m
< mi
and
Mi
< M
then, |
|
m
(b -
a)
= m
(Dx1
+
·
· ·
+ Dxn)
< s
and S
< M
(Dx1
+
·
· ·
+ Dxn)
= M
(b -
a), |
| that
is, the lower sum does not exceed the upper sum, both sums are bounded from
above and from below. |
| If we now repeat the process and continue to divide each subinterval
Dx into smaller intervals, so that the number of subintervals increases to infinity
(n
®
oo), that is, bases of the rectangles become smaller and smaller while the number of rectangles increases to infinity. |
| By passing to the infinitely small (infinitesimal)
interval Dx, each of two infinite sequences of numbers
S and
s
converge to a fixed
limit value. |
| That is, the sequence of areas of circumscribed rectangles will decrease toward the fixed limit value, as the number of intervals
increases, and the sequence of areas of inscribed rectangles will increase toward
that fixed limit
value. |
| Thus,
if the sequence of circumscribed rectangles S
and the sequence of inscribed rectangles
s
tends to the same limit
value I independent of the partition of the interval [a,
b],
provided the length of each subinterval tends
to zero while number of the partition
points tend to infinity, then the limit value I
equals the area A. |
| Therefore,
using the above notation we can write |
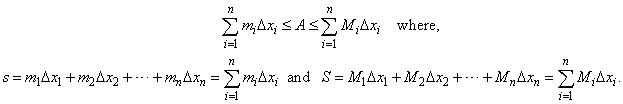 |
|
|
The definition of the
definite integral |
| Finally,
we say a function
f
is integrable on an interval [a,
b] if there exists a
unique number A
such that |
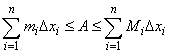 |
| for
any partition of [a,
b]. |
|
If
y = f (x)
is integrable on [a,
b]
then we call A
the definite integral of f
on [a,
b] and write |
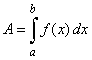 |
| where
∫ symbolize the sum, the function
f (x) is called
the integrand, the differential dx
shows that x
is the variable
of integration and, the numbers a
and b
are called the limits of integration (a
is the lower limit and b
is
the upper limit). |