|
|
Applications
of differentiation - the graph of a function and its derivatives |
 Finding and classifying
critical (or stationary) points, examples
Finding and classifying
critical (or stationary) points, examples |
|
|
|
|
|
|
|
| Finding and classifying
critical (or stationary) points examples |
| Example: Find
the extreme point of the quartic polynomial y
= x4 -
4x3 + 6x2 -
4x and sketch its graph. |
| Solution: To
rewrite given polynomial from general into translatable form, and this
way determine its source form,
we should always first calculate the coordinates of translation |
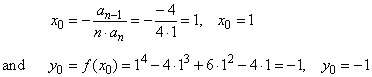 |
| then,
plug x0
and y0
into |
| y
+ y0 = a4(x + x0)4
+ a3(x + x0)3 + a2(x
+ x0)2 + a1(x +
x0) + a0 |
| to get the source form of the given polynomial |
| y
-
1 = 1· (x + 1)4 -
4(x + 1)3 + 6(x + 1)2 -
4(x + 1) + 0,
so the source function y
= x4. |
| Therefore,
we can write, y
= x4 -
4x3 + 6x2 -
4x
or y +
1 = (x -
1)4
or f (x)
= (x -
1)4 -
1. |
| To
find the extreme point, calculate the first derivative of the above
expression and set it to zero, |
| f
' (x) = 4(x -
1)3,
then f
' (x) = 0
or 4(x -
1)3 = 0
what yields x
= 1 |
| as
possible abscissa of the extreme point. |
| To
check if x =
1
is the abscissa of the extreme point, plug it into
successive higher order derivatives, starting with
the
second derivative. Thus, |
| f
'' (x) = 12(x -
1)2,
since f
'' (1) = 0
we must proceed with the higher order derivatives, so |
|
f
''' (x) = 24(x -
1)
and
f ''' (1) =
0
and finally f
IV (x) = 24 > 0 |
| confirms
x = 1
is the abscissa of the minimum as
first of higher order derivatives that do not vanishes
at this point
is of even order and positive. |
|
By plugging x =
1
into given quartic we find the
minimum
Tmin(1,
-1),
as
shows
the figure below. |
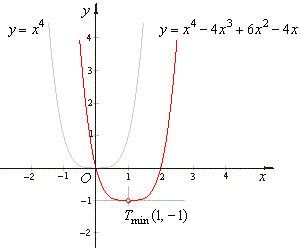 |
|
| Example: Find
extreme points and points of inflection of the quintic y
= -x5 +
5x4 -
7x3 + x2 +
4x
-1
and sketch its graph. |
| Solution: To
rewrite given polynomial from general into translatable form, and this
way determine its source form,
we first calculate the coordinates of translation |
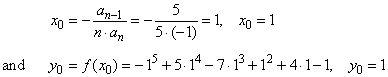 |
| then,
plug x0
and y0
into |
| y
+ y0 = a5(x + x0)5
+ a4(x + x0)4
+ a3(x + x0)3 + a2(x
+ x0)2 + a1(x +
x0) + a0 |
| to get the source form of the given polynomial |
| y
+ 1 = -
1(x + 1)5 + 5(x + 1)4 -
7(x + 1)3 + (x + 1)2 + 4(x + 1)
-
1, |
| what
after expanding and reducing gives y
= -
x5 + 3x3,
the source quintic. |
| Therefore,
we can write
y
= -x5 +
5x4 -
7x3 + x2 +
4x
-1 |
|
or y
-
1
= - (x -
1)5 + 3(x -
1)3 or
f(x)
= - (x -
1)5 + 3(x -
1)3 +
1. |
| To
find the extreme points, calculate the first derivative of the above
expression set it to zero and solve for x, |
| f
' (x) =
-
5(x -
1)4 + 9(x -
1)2 =
-
(x -
1)2 · [5(x -
1)2 -
9] |
| then
we set
f
' (x) = 0,
-
(x -
1)2 · [5(x -
1)2 -
9] = 0 |
|
what yields, x1
= 1,
x2
= 1 -
3/Ö5 and
x3
= 1 + 3/Ö5
as potential abscissas of the extreme points. |
| To
check if x1
= 1
is the abscissa of the extreme point, plug it into
successive higher order derivatives, starting with
the
second derivative. Thus, |
| f
'' (x) =
-
20(x -
1)3 + 18(x -
1) =
-
2(x -
1) · [10(x -
1)2 -
9]
since f
'' (1) = 0 |
|
we must proceed with the higher order derivatives, |
| f
''' (x) =
-
60(x -
1)2 + 18
so that f ''' (1) =
18
is not 0 |
| what
classifies root x1
= 1
as the abscissa of the point of inflection, as
first of higher order derivatives that do not vanishes
at this point is of odd order. |
| While
roots, x2
= 1 -
3/Ö5
and x3
= 1 + 3/Ö5
plugged into the second derivative respectively yield |
| f
'' (1 -
3/Ö5)
> 0,
so
x2
= 1 -
3/Ö5
is the abscissa
of the minimum
|
|
and f
'' (1 + 3/Ö5)
< 0,
so
x3
= 1 + 3/Ö5
is the abscissa
of the maximum.
|
| To
find points of inflection of the given quintic we set the second
derivative to zero and solve for x, |
| f
'' (x) = -
20(x -
1)3 + 18(x -
1),
-
2(x -
1) · [10(x -
1)2 -
9]
= 0 |
|
what yields, x1
= 1,
x2
= 1 -
3/Ö10
and x3
= 1 + 3/Ö10 as
possible abscissas of the points of inflection. |
| The
root x1
= 1
we've already classified
as the point of inflection. |
| Then
we plug roots, x2
= 1 -
3/Ö10 and
x3
= 1 + 3/Ö10
into the third derivative respectively |
| f
''' (x) = -
60(x -
1)2 + 18,
so
f ''' (1 -
3/Ö10)
¹
0
and
f ''' ( 1 + 3/Ö10)
is not 0 |
| what
classifies roots, x2
and x3
as the abscissas of the points of
inflection. |
| By
plugging the abscissas x1,
x2 and x3
into the given quintic we get the ordinates of the points of inflection. |
| The
graph of the given quintic polynomial and its source function is shown
in the figure below. |
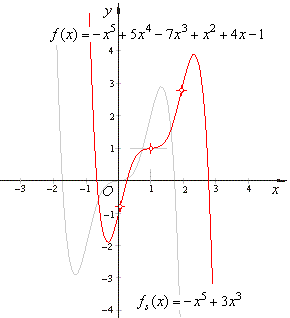 |
|
|
|
|
|
|