|
| Coordinate
Geometry (Analytic Geometry) in Three-dimensional Space |
|
|
|
|
Points, lines and planes in three-dimensional coordinate
system represented by vectors |
Equations of a line in space |
|
The
vector equation of a line
|
|
The parametric equations of a line
|
|
Equation of a line defined by
direction vector and a point - Symmetric equation of a line |
|
Line given by two points
|
|
Distance between two given points
|
|
Orthogonal projection of a line in
space onto the xy
coordinate plane |
|
A
line in a 3D space examples |
|
Angle between lines
|
|
Condition for intersection of two
lines in a 3D space
|
|
|
|
|
|
|
| Equations of a line in space |
| The
vector equation of a line
|
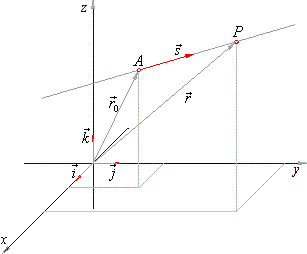
| Through a given point
A(x0,
y0, z0), which is determined by position vector
r0
= x0i + y0 j
+ z0k, passes a
line directed by its direction vector s
= ai + bj
+ ck. |
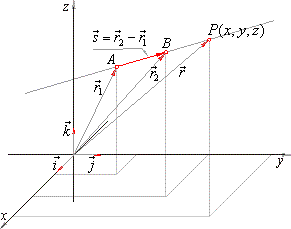
| Thus, the position of any point
P(x,
y, z) of a line is
then uniquely determined by a
vector |
|
|
| which is called the vector equation of a
line. |
| That is,
a radius vector r
= xi + y j
+ zk of every
point of the line, represents the sum of the radius vector r0,
of the
given point, and a vector t
· s collinear to the vector
s, where t
is a parameter which can take any real value
from -
oo
to +
oo
. |
|
 |
|
|
| The parametric equations of a line
|
| By writing the above vector equation of a line in
the component form
|
 |
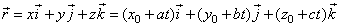| obtained are components of the vector
r, |
x
= x0 + at,
y = y0 +
bt and z
= z0 + ct |
which, at the same
|
|
| time, represent coordinates of any point of the line expressed as the function of a variable
parameter
t.
|
| That is why they are called the
parametric equation of a line.
|
|
| Equation of a line defined by
direction vector and a point - Symmetric equation of a line |
| Now,
let express t
from the above parametric equations
|
 |
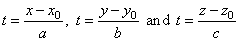| so, by equating
obtained is
|
|
|
| equation of a line passing through a point
A(x0,
y0, z0)
and given direction vector
s
= ai + bj
+ ck. |
| Scalar components (or the coordinates),
a,
b, and
c, of the direction vector
s, are |
|
|
| or the direction cosines
|
|
|
| That
is, the cosines of the angles that a line forms by the coordinates axes
x,
y
and
z, or the scalar
components of
the unit vector of the direction vector
s
|
|
|
|
| Line given by two points
|
| A line through points
A
and B, determined by their position vectors, |
| r1
= x1i + y1 j
+ z1k
and r2
= x2i + y2 j
+ z2k, |
| has the direction vector
s
= r2 -
r1 so that its vector equation is |
|
|
| If we write this equation in the component form that is |
 |
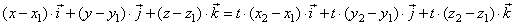| by equating corresponding scalar components |
 |
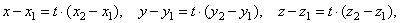| and by
eliminating parameter t |
|
|
| obtained is
equation of a line through two given |
| points, A(x1,
y1, z1)
and B(x2,
y2, z2). |
| The direction cosines are, |
 |
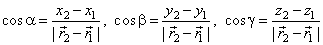| where |
 |
|
 |
|
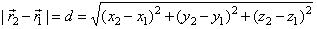| is the
distance between given points
A
and
B. |
| If, for example, in the above equation of a line through two points in a space, we take that
z
coordinate of both given points
is zero, we obtain known equation of a line through two points in a coordinate plane, i.e.,
|
 |
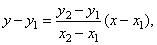| and at the same time,
it is the equation of the orthogonal projection of a line
in 3D space onto the xy
coordinate plane.
|
|
|
|
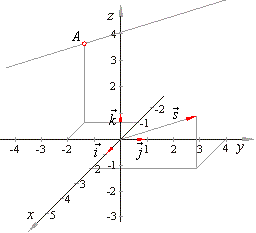
| Example:
Determine equation of a line passing through the point
A(-1,
-2, 3) and which is parallel to the
vector
s
= 2i + 4j + 2k.
|
| Solution: |
| By plugging coordinates of the given point A
and
the components of the direction vector s
into equation of a line |
 |
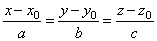| obtained is |
 |
|
 |
|
|
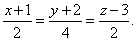| Example:
Find the equation of a line passing through the points,
A(1,
0, 2) and B(4,
5, 6).
|
| Solution: |
| By plugging coordinates of the given points into |
| equation of a line
through two given points |
 |
| obtained is |
 |
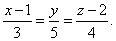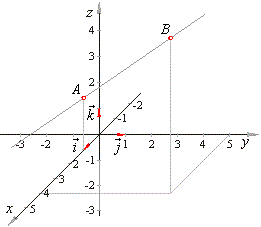
| Plug the coordinates of both points into obtained equation to verify
the result.
|
|
 |
|
|
| Example:
Find the angles that a line
|
 |
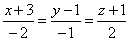forms with coordinate
axes
|
|
| Solution: The unit vector of the direction vector
s
= -2i
-
j + 2k |
 |
|
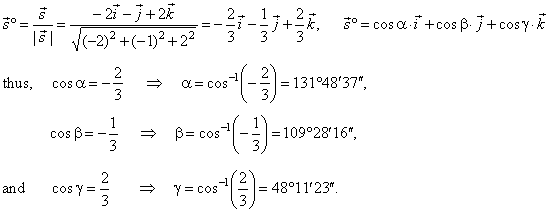| Angle between lines
|
| Angle between two lines |
 |
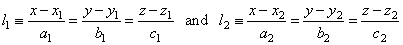equals the |
|
| angle
subtended by direction vectors, s1
and s2
of the lines |
|
|
| For the lines that do not intersects, i.e., for the skew lines (such as two lines not lying on the same plane in
space), assumed is the angle between lines that are parallel to given lines that intersect. |
| That is, the initial
points of their direction vectors always can be brought to the same point by translation. |
|
| Condition for intersection of two
lines in a 3D space
|
| Two lines in a 3D space can be parallel, can intersect or can be skew lines. |
| Two parallel or two intersecting
lines lie on the same plane, i.e., their direction vectors, s1
and s2 are coplanar with the vector
P1P2
= r2 -
r1 drawn
from the point P1,
of the first line, to the point
P2 of the second line. |
| Therefore, the scalar triple product of these
vectors is zero, |
|
|
|
| Example: Given are lines, |
 |
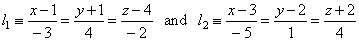examine whether |
|
| lines intersect or are skew lines, and if intersect, find the intersection point and the angle between lines. |
| Solution:
|
| In the given equations of lines, |
|
P1(1, -1,
4) and
s1
= -3i + 4
j -
2k,
|
| and |
|
P2(3, 2, -2)
and s2
= -5i +
j + 4k |
| therefore,
vector |
| P1P2
= r2 -
r1
= 2i + 3 j -
6k. |
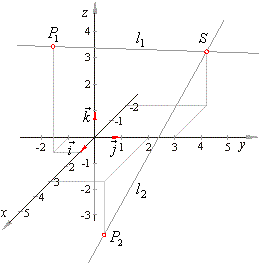
| Let
examine whether the lines intersect |
|
 |
|
 |
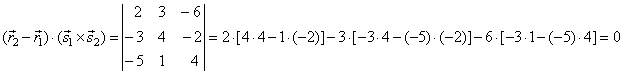| therefore,
the lines intersect. |
| Intersection of two lines is a point, coordinates of
which satisfy both equations therefore, solutions, x,
y
and z of the equations,
l1
and l2
are the coordinates of the intersection point, that is |
 |
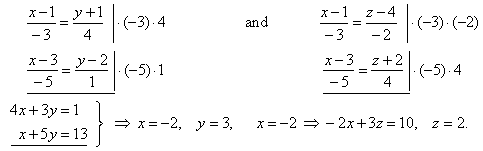| Thus, given lines intersect at the point
S(-2,
3, 2). |
| The angle between
direction vectors, s1
and s2
of the lines, we calculate from the formula |
 |
|
|
|
|
|
|
|
|
|
|
|
|
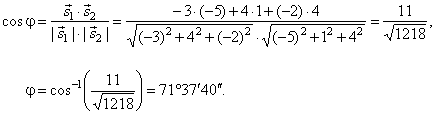| Coordinate
geometry contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
