|
| Coordinate
Geometry (Analytic Geometry) in Three-dimensional Space |
|
|
|
|
Plane
in a three-dimensional (3D) coordinate system |
Equations of
a plane in a coordinate space
|
|
The equation of a
plane in a 3D coordinate system |
|
The Hessian normal form of the
equation of a plane
|
|
The intercept
form of the equation of a plane |
|
| |
|
|
|
|
| Equations of a plane in a coordinate space
|
| The equation of a
plane in
a
3D coordinate system |
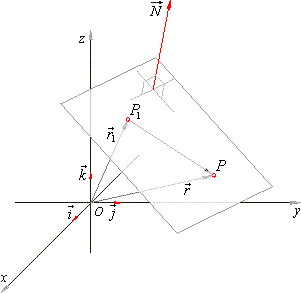
| A plane in space is defined by three points (which don’t all lie on the same line) or by a point and a normal
vector to the plane. |
| Then, the scalar product of the vector
P1P
= r -
r1, drawn from the
given point P1(x1,
y1, z1) of the plane to any point
P(x,
y, z)
of the plane, and the normal vector N
= Ai + Bj
+ Ck, is zero, that is |
| |
 |
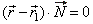which is called the vector equation of a
plane. |
|
|
Or,
|
 |
|
|
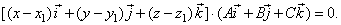| Therefore, |
| (x
-
x1)
· A
+ (y -
y1)
· B
+ (z -
z1)
· C
= 0 |
| giving |
A
· x
+ B · y
+ C · z
+ D = 0 |
|
|
|
where, D
=
-
(Ax1+
By1+
Cz1) |
|
the general equation of a plane in 3D
space. |
| If plane passes through the origin
O
of a coordinate system then its coordinates, x =
0, y
= 0, and z
= 0 plugged into the equation of the plane, give |
| A
· 0
+ B · 0
+ C · 0
+ D = 0 => D = 0. |
| Thus, the condition that plane passes through the
origin is D
= 0. |
|
 |
|
|
| The Hessian normal form of the
equation of a plane
|
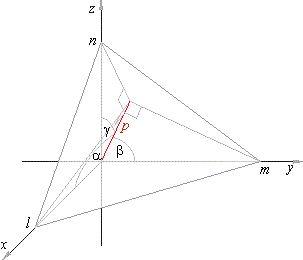
| Position of a plane in space can also be defined by the length of the normal, drawn from the origin to the plane
and by angles,
a, b and
g, that the normal forms with the
coordinate axes.
|
| If
N°
is the unit vector of the normal then its components are, cosa,
cosb
and
cosg.
|
| Then the projection of the position vector
r, of any point
P(x,
y, z) of the plane, onto the normal has the length
p. |
| Since the projection is determined by expression |
 |
| that is,
r
· N°
= p or
written in the coordinates |
| |
x
· cosa
+ y · cosb
+ z · cosg
-
p = 0 |
|
|
| represents the
equation of a plane in the Hessian
normal
form. |
|
 |
|
|
| The intercept form of the equation of a
plane
|
| If,
l,
m
and n
are the intercepts of
x,
y
and z
axes and a plane respectively, then projections of these segments in
direction of the normal drawn from the origin to the
plane are all equal to the length of the normal, that is
|
 |
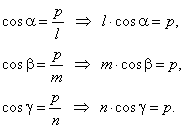| By plugging these values of cosines into Hessian normal
form of the equation of plane, obtained is
|
|
|
| the intercept form of the equation of plane. |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
| Coordinate
geometry contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
