|
| Coordinate
geometry or Analytic geometry |
|
|
|
|
Line in a coordinate plane
|
Hessian normal form of the equation of a line |
|
Distance between a point and a line |
|
Lines and
points relations, examples
|
|
|
|
|
|
|
|
|
|
Hessian normal form of the equation of a line
|
|
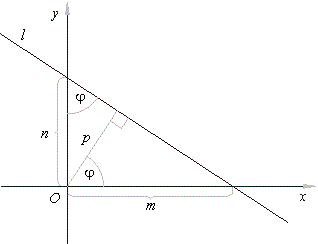
The normal p
from the origin to a line subtends the angle j
with the x-axis
and form two right triangles with axes as is shown in the figure below,
then
|
 |
 |
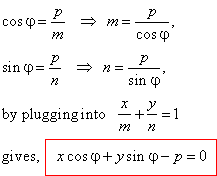| Hessian
normal form of the equation of a line. |
|
|
|
By comparing the normal form with the
general form Ax
+ By + C = 0, of the
equation of the line, we can find relations between corresponding
coefficients of both forms so, if we write
|
|
lAx
+ lBy
+ lC
= 0
|
|
and after comparing both
equations, lA
= cosj
and lB
= sinj
|
|
|
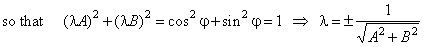
then, by plugging into the general
form obtained is
|
|
|
|
the normal form of the equation of a
line expressed by coefficients of the general form, where the sign of the
square root should be opposite to the
sign of
C.
|
|
|
|
|
|
Distance between a point and a line
|
|
The distance from a point
A(x0,
y0) to a line
l, equals the distance between the given line and a line passing
through the given point parallel to
the given line, as shows the figure below.
|
|
So, the length of the normal from the origin
to that new line is p +
d, and the coordinates of
A will then satisfy equation of the line, that is
|
|
x0 cos
j
+ y0 sin
j
= p +
d or |
| d
= x0 cos
j
+ y0 sin
j
-
p. |
|
If equation of a line is given in the general form, then the distance is
|
|
|
| The sign of the square root is taken to be opposite to
sign of
C, and
where the negative result shows that the given point is at
the same side as the origin in relation to the given line.
|
|
 |
|
|
|
|
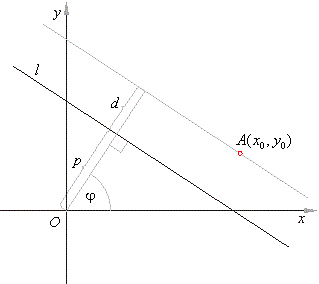Example:
Given is a point A(-2, 3) and the direction vector of a line
s = i
-
2j, determine equation of the
line through the point
A
and draw a diagram.
|
|
Solution:
Plug the point A
and the components of the direction vector into the parametric equation of a line:
|
|
|
|
|
|
Example:
Write equation of a line in the point slope form and in parametric form if the line passes through
the point A(2,
-1) and whose slope
m = -3, draw a diagram.
|
|
Solution:
Plug the given elements of the line into equation
|
|
|
|
|
|
Example:
A line passes through points
A(-3,
-4) and
B(9,
4). Find the general form of its equation and
the segments that the line cuts on the coordinate axes.
|
|
Solution:
From the equation of a line through two points
|
|
|
|
|
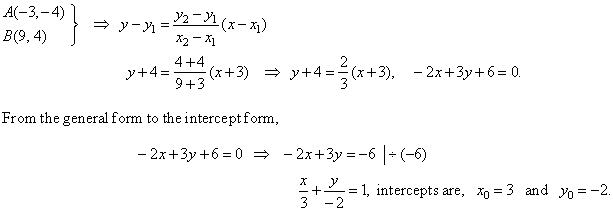
Example:
Check if points, A(2,
-1),
B(5, -5) and
C(-1,
3) all lie on the same line.
|
|
Solution:
If given points lie on the same line then must be satisfied following condition
|
|
|
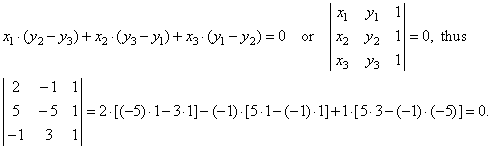
Check can also be done by examining if given points satisfy
vector’s equation
|
|
|
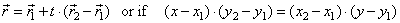
by taking coordinates of any of three given points as the coordinates of the radius vector r.
|
|
|
|
Example:
A line through a point A(-3,
5) forms a triangle with the coordinate axes whose area is 24
square units, find equation of the line.
|
|
|
| Solution:
Area of a triangle |
 |
|
|
|
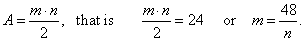Coordinates of the point
A
must satisfy equation of the line
|
|
|
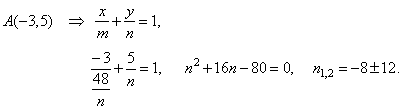
The solution n
= 4 satisfies given conditions, so that
|
|
|
|
|
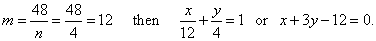
Example:
Find the distance of the line -4x
+ 3y -
25 = 0 from the origin.
|
|
Solution:
Rewrite the equation of given line from the general form to the normal form,
that is
|
|
|
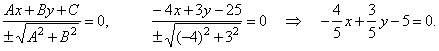
Comparing with the normal form xcosj +
ysinj
-
p = 0, follows that the distance
p = 5.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Coordinate
geometry contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
