|
| Coordinate
geometry or Analytic geometry |
|
|
|
|
Line in a coordinate plane
|
 The parametric equations of a line
The parametric equations of a line |
 Parallel and perpendicular lines
Parallel and perpendicular lines |
|
|
|
|
|
|
|
|
|
The parametric equations of a line
|
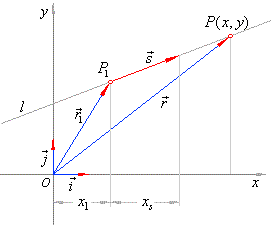
| If
in a coordinate plane a line is defined by the point P1(x1,
y1) and the
direction vector s
then, the position (or
radius)
vector r
of any point P(x,
y) of the line |
| r
= r1 + t · s,
-
oo
< t < + oo
and
where, r1
= x1i + y1 j
and s
= xsi + ys j, |
| represents the vector's equation of the line. |
| Therefore,
any point of the line can be reached by the radius vector |
| r
= xi + y j
= (x1 + xst) i
+ (y1 + yst) j |
| since the scalar quantity t
(called the
parameter) can take any real value from -
oo
to + oo. |
| By
writing the scalar components of the above vector's equation obtained is |
| x
= x1 + xs · t |
| y
= y1 + ys · t |
|
|
| the parametric
equations of the line. |
|
 |
|
| To
convert the parametric equations into the Cartesian coordinates solve
given equations for t.
So |
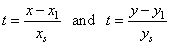 |
| by
equating |
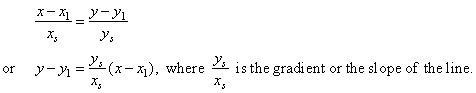 |
|
| Therefore,
the parametric equations of a line passing through
two points P1(x1,
y1) and P2(x2,
y2) |
| x
= x1 + (x2 -
x1) t |
| y
= y1 + (y2 -
y1) t |
|
|
|
| Parametric
curves have a direction of motion |
| When
plotting
the points of a parametric curve by increasing t, the
graph of the function is traced
out in the direction of motion. |
|
| Example: Write
the parametric equations of the line y
= (-1/2)x
+ 3 and sketch its graph. |
| Solution: Since |
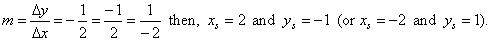 |
|
|
| Let
take the x-intercept
as point P1, so |
| for
y
= 0 => 0 = (-1/2)x
+ 3, x
= 6 therefore,
P1(6,
0). |
| Substitute
the values, x1
= 6, y1
= 0, xs
= 2,
and ys
= -1
into the parametric equations of a line |
| x
= x1 + xs · t,
x
= 6 + 2t |
|
y
= y1 + ys · t,
y = -t |
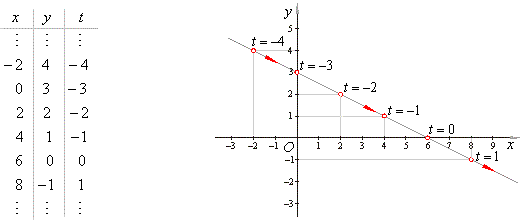 |
|
The direction of motion (denoted by red arrows) is given by increasing t. |
|
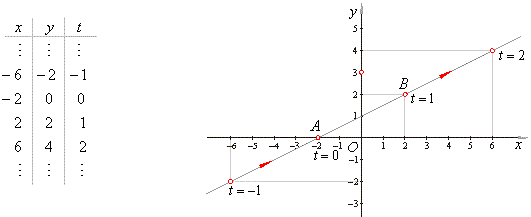
| Example: Write
the parametric equations of the line through points, A(-2,
0) and B(2,
2) and sketch the graph. |
| Solution: Plug the coordinates x1
= -2, y1
= 0, x2
= 2, and y2
= 2
into the parametric equations of a line |
|
x
= x1 + (x2 -
x1) t,
x
= -2
+ (2 + 2) t
= -2 +
4t,
x
= -2 +
4t, |
|
y
= y1 + (y2 -
y1) t,
y = 0
+ (2 -
0) t
= 2t,
y
= 2t. |
| To
convert the parametric equations into the Cartesian coordinates solve |
| x
= -2 +
4t for t
and plug into y
= 2t |
|
therefore, |
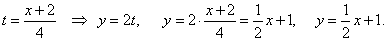 |
|
|
 |
|
| Parallel and perpendicular lines |
| Two
lines having slopes m1
and m2
are parallel if |
| |
m1
= m2 |
|
that
is, if they have the same slope. |
|
|
| To
find the criteria two lines, y
= m1x
and y
= m2x
to be
perpendicular or orthogonal we can
use the principle of similar triangles, OA'A
and OB'B
shown
in the picture. |
| Therefore, |
m1
: 1 =
-1
: m2 |
=> |
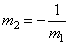 |
|
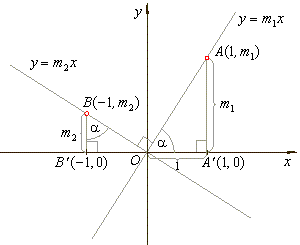 |
|
|
| This
relation will stay unchanged if we translate the perpendicular
lines, that is, when lines |
|
y = m1x
+ c1
and y
= m2x
+ c2
are written in the slope-intercept form. |
| Two
lines are perpendicular if the slope of one line is the negative
reciprocal of the other. |
|
| Example:
Find the equation of the line that is perpendicular to
the line |
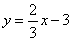 |
and passes
through |
|
| the point A(-2,
5). |
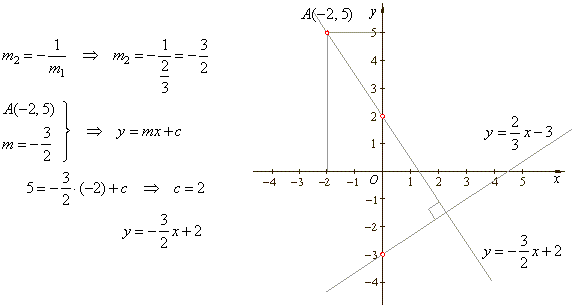 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Coordinate
geometry contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |