|
| The
Set of Real Numbers - The Real Number System |
|
|
|
Interval definition and notation |
|
Distance
and absolute value |
|
Distance between two numbers |
|
Properties of absolute value |
|
Midpoint formula for the real
number line |
|
|
|
|
|
|
|
Interval
Definition and Notation |
| An
interval is the set containing all real numbers (or points)
between two given real numbers, a
and
b,
where a
<
b. |
| A
closed interval [ a,
b ]
includes the endpoints, a
and
b,
and it corresponds to a set notation { x
| a
<
x
<
b },
while an open interval (a,
b) does
not include the endpoints. |
| On
the real line, the half-closed (or half-opened) interval
from a
to b
is written [a,
b)
or (a,
b],
where square brackets indicate inclusion of the endpoint, while
round parentheses denote its exclusion. |
| Thus,
[ a,
b ]
= { x
| a
<
x
<
b }
- a closed interval |
|
[ a,
b )
= { x
| a
<
x
<
b }
- an interval closed on left, open on right |
|
( a,
b ]
= { x
| a
< x
<
b }
- an interval open on left closed on right |
|
( a,
b )
= { x
| a
<
x
<
b }
- an open interval |
|
| Unbounded
intervals or intervals of infinite length are also written
in this notation, thus [ a,
oo
) is unbounded interval x
> a,
which is regarded as closed, while (a,
oo
) is the open interval x
> a
and where oo
denotes infinity.
|
|
Hence,
(
− oo
, a
]
= { x
| x
<
a }
and [ a,
oo )
= { x
| x
>
a },
|
|
(
− oo
, a)
= { x
| x
< a
} and ( a,
oo )
= { x
| x >
a }.
|
|
The real line R
= (
−
oo
, oo
).
|
|
|
| Distance
and absolute value |
| The
distance between a number x
and 0 equals x
if x
>
0, and equals −
x
if x
<
0,
therefore the absolute value of a number
x, denoted
| x |, is x
if x
>
0, and −
x
if x
<
0. |
| From
the definition of the absolute value it follows that the
distance between two numbers a
and b, |
|
|
| |
| Properties of absolute value |
Examples: |
| 1 |
 |
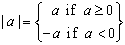1 |
 |
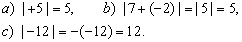| 2 |
 |
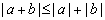2 |
 |
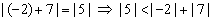| 3 |
 |
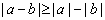3 |
 |
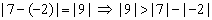| 4 |
 |
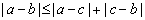4 |
 |
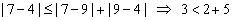| 5 |
 |
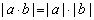5 |
 |
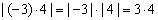| 6 |
 |
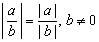6 |
 |
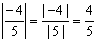| 7 |
 |
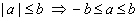7 |
 |
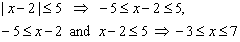| 8 |
 |
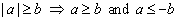8 |
 |
|
|
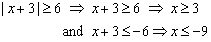| The
Midpoint Between Two Numbers |
| Suppose
x1and
x2
are given numbers and x1<
x2,
and let xM
be the midpoint. Therefore, |
|
x1<
xM
< x2
and d(x1,
xM)
= ½
·
d(x1,
x2). |
| Then,
d(x1,
xM)
= | x1−
xM
|
and d(x1,
x2)
= | x1− x2
| |
|
= xM
−
x1,
since x1
< xM
= x2− x1,
since x1
< x2 |
| by
plugging into above equation, xM
−
x1
= ½
· ( x2− x1) |
| and
solving for xM
gives: |
xM
= ½
· ( x1+
x2) |
-
the midpoint formula for the real line |
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
