| |
| The
Set of Real Numbers - The Real Number System |
| |
|
|
| |
|
Sets
of
Numbers: |
Natural numbers |
|
Whole numbers |
|
Integers |
|
Rational numbers |
|
Irrational numbers |
|
Real numbers |
|
The
real number line and relations |
|
One-dimensional coordinate system |
|
Unit
interval |
|
Relations,
less than and greater than |
|
|
|
|
|
|
| Sets
of
Numbers: |
| The set of
natural numbers |
|
N = {1, 2, 3, . . . , n,
n
+ 1, . . . }, the positive integers used for counting. |
|
| The
set of whole numbers |
|
N0
= {
0, 1, 2, 3, . .
. }, is just like the set of natural numbers except that it also
includes zero. |
|
| The set of
integers |
|
Z
= {
. . . , −3,
−2,
−1,
0, 1, 2, 3, . . . }, consists of all natural numbers, negative whole numbers and |
|
zero. This means that the set of natural numbers is a subset of
integers, i.e., N
is a subset
Z. |
|
| The set of
rational numbers |
|
Q
= {
a/b
| a,
b
Î Z,
b
is not
0 }, is the set of all proper and improper fractions. That is, a ratio or |
| quotient of two
integers a
and b, where
b
is not zero. |
| All integers are in this set since every integer a
can be expressed as the fraction a/1
= a.
Thus, the set of all natural numbers
N is proper subset of integers
Z
and the set of integers is proper subset of the set of rational
numbers, N is a subset
Z is a subset
Q.
Rational numbers can be represented as integers, fractions, terminating decimals and recurring or repeating decimals. |
| |
| The set of
irrational numbers, denoted I, is the set of numbers that
cannot be written as ratio of two integers. |
|
An irrational number expressed as a decimal never repeat or terminate. The irrational numbers are precisely those numbers whose decimal expansion never ends and never enters
a periodic pattern, such as 0.1020030004..., p,
Ö2, Ö3, or any root of any natural number that is not a perfect root is an irrational number.
|
| The set of
real numbers, denoted R,
|
R =
Q U I |
| is
the set of all rational and irrational numbers, R =
Q U I.
The real numbers or the reals are either rational or
irrational and are intuitively defined as numbers that are in one-to-one correspondence
with the points on an infinite line, the number line. |
 |
|
|
|
The Real Number Line, and Relations |
|
|
 |
|
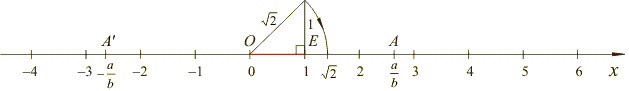| The real number line is an infinite line on which points are taken to represent the real numbers by their distance from a fixed point labeled
O and called the
origin. |
| We
use the variable x
to denote a one-dimensional coordinate system, in
this case the number line is called the x-axis. |
| The line segment
OE
denotes
unit length, that is, | OE
|
= 1. The absolute value (or modulus) of a real number
x,
denoted | x | is its numerical value without regard to its sign. |
| For example,
| + 5 | = 5 and | −
5 | = 5, and 0 is the only absolute value of 0.
The absolute value of a real number a
is its distance from the origin. |
|
|
| The
unit interval is the interval
[ 0, 1 ] that is the set of all real
numbers x such that
0 ≤
x ≤
1, we say x
is greater than or equal to zero
and
x
is less than or equal to one, meaning x
is between 0 and 1 including the endpoints. |
|
|
| A rational number
-
a/b,
in the above picture,
corresponds to the point A'
which is symmetrical regarding the origin to the point
A, which
denotes the rational number
a/b. |
| Therefore,
| OA | = |
OA' |
= a/b
· | OE
|
= a/b.
|
| For
each real number x,
there is a unique real number, denoted −x,
such that x
+ ( − x
) = 0. In
other words, by adding a number to its negative or opposite, the
result is 0. |
| Every point of the number line corresponds to one real number. |
|
|
| Relations,
less than and greater than |
| Let
a
and b
are distinct real numbers. We
say that a
is less than b
if a
− b
is a negative number, and write a
< b, i.e.,
a
< b
means a
− b
is negative. |
| On
the x-axis,
a
< b
is represented as the number a
lies to the left of b. |
| We
say that a
is greater than b
if a
− b
is a positive number, and write
a
> b, i.e.,
a
> b means a
− b
is positive. On
the x-axis,
a
> b
is represented as the number a
lies to the right of b. |
| Similarly,
a
≤
b
denotes that a
is less than or equal to b,
and a
>
b,
a
is greater than or equal to b. |
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
