|
| Rational Numbers
|
|
|
|
Definition |
|
Comparing rational numbers
|
|
Equivalent fractions |
|
Reducing or simplifying fractions |
|
Adding and subtracting rational
numbers or fractions
|
|
Multiplication of
rational numbers |
|
Reciprocal fractions, multiplicative inverse |
|
Division of
rational numbers |
|
Simplifying complex or compound
fractions |
|
|
|
|
|
|
| Definition |
| A
rational number is a ratio or quotient of two integers, usually written
as the vulgar fraction a/b, where
b
is
not zero. The set of all rational numbers is denoted as |
| Q
= { a/b
| a,
b
Î
Z,
b is
not 0 }. |
| A rational number or a fraction
a/b
denotes the result of dividing a
by b, i.e.,
a/b
= a ¸
b, b
is
not 0. |
|
All integers are rational numbers as they can be written as a fraction with a denominator of 1. |
|
Terminating decimals and recurring decimals are rational numbers as they can be written
as fractions. |
|
Not all decimals are rational numbers, since not all decimals can be written as fractions. |
|
|
A rational number is positive if its numerator and denominator are both positive integers or both
negative integers. A rational number is negative if its numerator and
denominator have different signs, that is,
|
 |
|
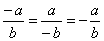| Examples: |
|
 |
|
|
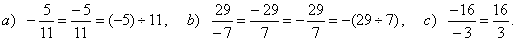| Comparing rational numbers
|
| A positive rational number
a/b =
r corresponds to a point
P(r) of
the real number line, symmetrically regarding the origin O, an
opposite number −
a/b corresponds to a point
P(−r). A rational
number r1
is less than a rational number
r2 if lies to the left of
r2 on
the number line, written r1
< r2. |
| |
 |
|
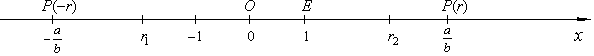| Two
rational numbers, |
 |
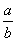and |
 |
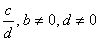are
equal, i.e., |
 |
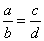if |
a
· d
= b
· c. |
|
|
| If the numerators
a and
c
both are integers and the denominators b
and d
both are natural numbers then; |
| |
 |
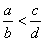if |
a
· d
< b
· c |
or |
 |
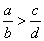if |
a
· d
> b
· c. |
|
|
| Examples: |
|
 |
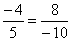since
(-4)
· (-10)
= 5
· 8 |
|
 |
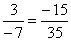since
3 · 35 = (-7)
· (-15) |
| |
|
 |
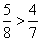since
5 · 7 > 8 · 4 |
|
 |
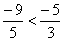since
(-9)
· 3 < 5
· (-5) |
|
|
|
Equivalent fractions |
| Convert a rational number or fraction to an equivalent fraction by multiplying the numerator and denominator by the same nonzero
number. |
| Equivalent
fractions are different fractions that represent the same
number. |
 |
| Examples: |
|
 |
|
|
| Reducing
or simplifying fractions |
| To reduce or simplify a fraction to lowest terms, divide the
numerator and denominator by their greatest common divisor (gcd)
or (greatest common factor - gcf). |
 |
|
| Examples: |
|
 |
|
|
| Adding and subtracting rational
numbers or fractions
|
| Find the least common denominator, write equivalent fractions, then
add or subtract the fractions. Reduce if necessary. |
|
| Examples: |
|
 |
| |
|
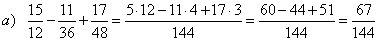12 = 2 · 2 · 3, 36 = 2 ·
2 · 3 · 3, 48 = 2 · 2 ·
2 · 2 · 3 |
| |
|
LCD(12, 36, 48) = 2 · 2 · 2 · 2 · 3 · 3 = 144 |
| |
|
 |
|
|
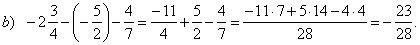| Multiplication of
rational numbers |
| Rational numbers are multiplied by multiplying
numerators and multiplying denominators. Change any mixed numbers to improper fractions. Reduce fractions before
multiplication. |
 |
|
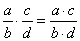| Examples: |
|
 |
|
|
|
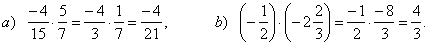Reciprocal fractions, multiplicative inverse |
| Two rational numbers different from zero are reciprocal
or multiplicative inverse if their product is unity. |
| Thus, the reciprocal of a fraction |
|
|
|
|
| Division of
rational numbers |
| Dividing a rational number or fraction by another
fraction is equivalent to multiplying the dividend with the reciprocal of the divisor.
|
 |
|
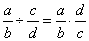| Examples: |
|
 |
| |
|
 |
|
|
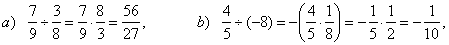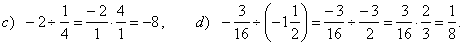| Simplifying complex or compound
fractions |
| A complex or compound fraction is a fraction whose numerator
and/or denominator are also a fraction or mixed number.
Divide the numerator by the denominator.
|
 |
|
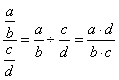| Examples: |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
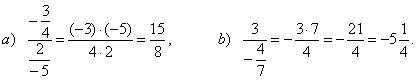| Beginning
Algebra Contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
