|
| Ratios and Proportions
|
|
|
|
Proportionality
|
|
Graphical representation of
proportionality
|
|
Proportion practice problems, use
of the rule of three
|
|
|
|
|
|
|
| Proportionality
|
| Two related variable quantities
x
and y
whose ratio is constant are called proportional or directly
proportional, written y
:
x =
m. |
| That is,
y =
m
· x ,
where m
(m > 0) is called the constant of proportionality,
related quantities x and
y are proportional if their corresponding
values are a constant multiple of each other. |
| Or, by whatever ratio
one quantity changes, the other changes in the same ratio. |
| It is also
called linear relationship. |
|
| Graphic representation of
proportionality
|
| If
x and
y
are proportional quantities, i.e., y
:
x =
m
then, their
corresponding values x1,
y1 and
x2,
y2 are also proportional
alternately |
|
x1
:
x2 =
y1
:
y2
that is, x1
is to
x2
as is
y1
to
y2 . |
| Given four
related variable quantities are Cartesian-coordinates of the points
P1
and
P2
of a straight line shown below: Thus, |
|
|
|
| Proportion practice problems,
use of the rule of three
|
| Linear relationship of two variable quantities whose ratio is constant,
show the proportions |
| x1
:
y1 =
x2
:
y2
or x1
:
x2 =
y1
:
y2 |
| we use
to solve practice problems. |
| Two quantities are in direct proportion,
or in linear relationship, when they increase or decrease in the
same ratio. Or, by whatever ratio one quantity changes, the other
changes in the same ratio. |
| If any three terms in a proportion are
given, the fourth may be found using the principles of solving equations. |
|
| Example:
A lift reaches the third floor in seven seconds. When will reach
the 18th floor? |
| Given quantities make the proportion |
| |
x1
:
y1 =
x2
:
y2, |
that
is, |
3
:
7 =
18 :
x |
=> |
 |
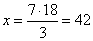seconds. |
|
|
| We could obtain the same result by setting up the corresponding
values of the proportional physical quantities in a table. |
| Values of the
same physical quantity (the same units) put in the first colon and the corresponding values
of another quantity in the second
colon. The arrows show the sequence of the terms of the
proportion. |
 |
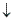x1 |
|
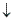y1 |
|
|
| x2 |
y2 |
or |
x1
:
x2
=
y1
:
y2 |
|
| Thus, for the values from the above example follows: |
| |
|
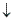3rd
floor |
|
|
7
sec. |
|
|
| |
18th
floor |
|
x
sec. |
or |
3
:
18 = 7 :
x |
|
| |
|
|
| => |
|
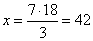seconds. |
|
|
|
| Example:
To
the central angle a = 30°, of a circle of radius
r, corresponds
the arc length equal
p/6
r. |
| What arc length corresponds to the
central angle a = 320°? |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
