|
| Plane Geometry - Plane Figures (Geometric
Figures) - Triangles |
|
|
|
|
|
Triangles |
Types of triangles
|
|
Main
properties of triangles
|
|
Congruence of triangles
|
|
Theorems about congruence
|
|
Similarity
of triangles, division of a line segment in a given ratio |
|
Similarity criteria of triangles
|
|
Area of a triangle
|
|
|
|
|
|
|
|
|
| Types of triangles
|
| Types of triangles categorized by their sides
are; a scalene triangle, isosceles triangle and
equilateral triangle. |
 |
|
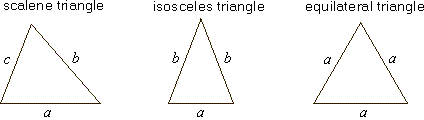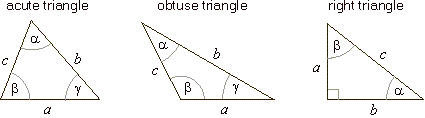
| The types of triangles categorized by their angles
are; an acute triangle, obtuse triangle and
right triangle. |
|
|
| Main
properties of triangles
|
| 1) A sum of triangle angles
a +
b
+ g
= 180°. |
| 2)
Angles lying
opposite the equal sides are also equal, and inversely. |
| All angles in
an equilateral triangle are also equal. It follows, that each angle in an
equilateral triangle is equal to 60 degrees. |
|
|
 |
|
|
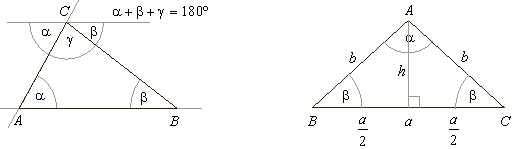3) In any triangle, if one
side is extended, the exterior angle is equal to a sum of interior
angles, not supplementary.
|
| The
sum of exterior angles is 360°. |
| 4)
Any side of a triangle is less than a sum of two other sides and
greater than their difference. |
| 5)
An angle lying opposite the greatest side, is also the greatest
angle, and inversely. |
| Proof:
By turning the side BC,
of the scalene triangle ABC
below, around the vertex C
by the angle g
into
direction of the side AC,
obtained is the isosceles triangle BCD
with equal angles on the base BD.
|
| Its
lateral side CD
< AC.
Angle a <
b', as b'
is the exterior angle of the triangle ABD,
and b'
< b,
therefore
a <
b. Thus, proved is the above
statement.
|
|
|
 |
|
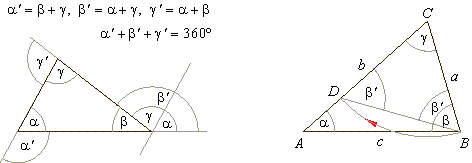| Congruence of triangles
|
| Two
figures are called congruent if they have identical size and shape, i.e., if their corresponding angles and sides are equal. |
| The
two congruent figures fit on top of each other exactly. We prove the
congruence of two figures by rotation and translation. |
| Theorems about congruence of triangles are; Two triangles are
congruent: |
| 1) If a pair of corresponding sides and the included angle
are equal SAS (Side-Angle-Side). |
| 2) If their corresponding sides
are equal SSS. |
| 3) If a pair of corresponding angles and the included
side are equal ASA. |
| The congruence of two triangles we denote as
D ABC
@
D A'B'C'. |
|
| Similarity of triangles,
division of a line segment in a given ratio
|
| Two plane figures are similar if differ in scale not in shape. |
| Two
polygons are similar, if their angles are equal and sides are proportional. |
| Similarity criteria of triangles are; Two triangles are
similar: |
| 1) If all their corresponding angles are
equal. |
| 2) If all their
sides are proportional. |
| 3) If one angle of a triangle is congruent to
one angle of another triangle and the sides that include those angles are proportional. |
| Similarity of
two triangles is denoted as D
ABC ~
D A'B'C'. |
|
 |
|
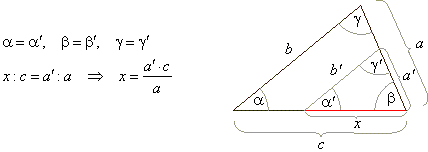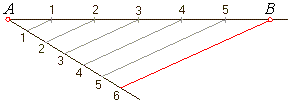
| Division of a line segment
AB to
equal parts: Example:
|
 |
|
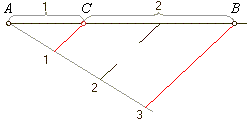
| Division of the line segment
AB
in a given ratio: Example:
AC
: BC
= 1 : 2 |
 |
|
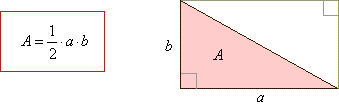
| Area of a triangle
|
| The area
A
of any triangle is equal to one-half the product of any base and corresponding height
h. |
| A height or
altitude of a triangle is a straight line through a vertex and perpendicular to the opposite
side. |
| This opposite side is called the
base of the altitude, and the point where the altitude intersects the base (or its
extension) is called
the foot of the altitude. |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
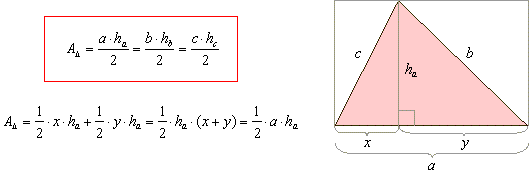| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
