|
| Algebraic
Expressions |
|
|
|
|
Right-angled
Triangle
- The Pythagorean Theorem |
The
Pythagorean theorem |
|
Trigonometric functions of an acute angle defined in a right triangle
|
|
|
|
|
|
|
|
| Right-angled
Triangle
- The Pythagorean Theorem |
| The
Pythagorean theorem
|
| In any right triangle the area of the square whose side is the
hypotenuse (the side of the triangle opposite the right angle) is equal
to the sum of the areas of the squares on the other two sides (legs). |
|
 |
|
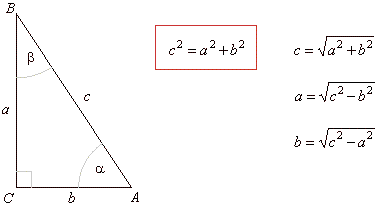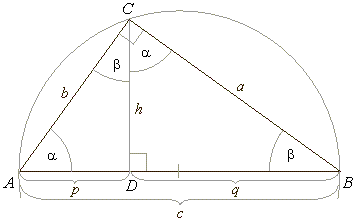
| From the similarity of the triangles,
ADC,
BDC
and ABC, and
Thales’ theorem (an angle inscribed in a semicircle is a right angle)
proved is Pythagoras’ theorem: |
|
 |
|
 |
|
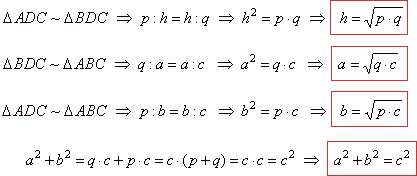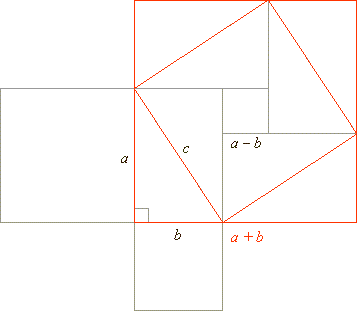
| In
the figure below shown are two geometric proofs of Pythagoras'
theorem which claims that the area of the square of the
hypotenuse (the side opposite the right angle) is equal to the
sum of areas of the squares of other two sides, i.e.,
c2
= a2
+ b2. |
|
First proof shows that the area of the
biggest red square with the side
a +
b is equal to the sum of
four equal right triangles and the square of the hypotenuse
c, therefore |
|
(a
+
b)2
= 4
· 1/2 · ab
+ c2 |
|
a2
+
2ab
+ b2
= 2ab
+ c2 |
|
a2+
b2
= c2 |
|
|
| Second
proof shows that the area of the square of the hypotenuse
c
is equal to the sum
of the same four right triangles and the area of the small square with side a
- b, therefore |
|
c2 = 4
· 1/2 · ab
+ (a
-
b)2 |
|
c2 = 2ab
+ a2
-
2ab
+ b2 |
|
c2 =
a2+
b2 |
|
|
|
 |
|
| Trigonometric functions of an acute angle defined in a right triangle
|
| Trigonometric functions of an acute angle are defined in a right triangle as a ratio of its
sides. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
