|
|
|
|
Integral
calculus
|
|
|
|
The definition of the
definite integral
|
| Finally,
we say a function
f
is integrable on an interval [a,
b] if there exists a
unique number A
such that |
|
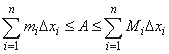 |
for
any partition of [a,
b]. |
|
|
If
y = f (x)
is integrable on [a,
b]
then we call A
the definite integral of f
on [a,
b] and write |
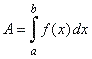 |
| where
∫ symbolize the sum, the function
f (x) is called
the integrand, the differential dx
shows that x
is the variable
of integration and, the numbers a
and b
are called the limits of integration (a
is the lower limit and b
is
the upper limit). |
|
|
Riemann
sum
|
| Until
now, in the definition of the sums, S
and s
we've used the maximum and the minimum values, Mi
and mi
of a given continuous function
f, so that mi
< f (x)
< Mi for x
in [xi
-
1, xi],
i = 1, 2 , . . . , n. |
| Now,
if we arbitrarily choose a point xi'
in every interval Dxi
and make products f (xi' )
Dxi,
then |
| mi
Dxi
<
f (xi' )
Dx
< Mi
Dxi,
i = 1, 2 , . . . , n and
by adding up |
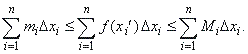 |
| The
left-hand and right-hand sides of the above inequality are the sums, s
and S
respectively that, because of continuity of f,
tend to the same limit value I
when the number
of subintervals n
increases to infinity, such that the length of
every interval Dxi
tends to zero, for any partition of the interval [a,
b]
and arbitrarily chosen
points xi'
in the subintervals [xi
-
1, xi].
Hence,
the middle term |
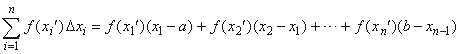 |
| called
a Rieman sum, will tend to the same limit value.
|
| Therefore,
if f
is a positive continuous function on the interval [a,
b] then, the definite
integral of the function from a
to b
is defined to be the limit
|
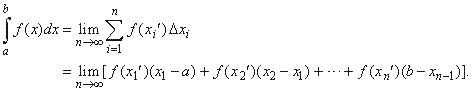 |
| Note
that the limit value of the sum changes as the number
of subintervals n
increases to infinity while the length
(Dxi)
of each tends to zero, for any partition of the interval [a,
b].
|
|
|
Calculating
a definite integral from the definition
|
|
As the sequence of inscribed rectangles s
tends to the definite
integral increasingly while the sequence of circumscribed rectangles S
tends to the same value decreasingly then |
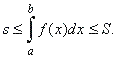 |
| Thus,
we
can approximate the area under the graph of a function over the interval
[a,
b]
to any desired level of accuracy using
the Riemann sum of inscribed or circumscribed rectangles. |
| The
area of the ith
rectangle f (xi' )
Dxi,
denoted as height times base, represents the ith
term of Riemann sum
and is called the element of area. |
| When
we use the partition of the interval [a,
b] into n
equal subintervals (regular partition) then |
|
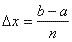 |
be
the length of the intervals [xi
-
1, xi],
i = 1, 2 , . . . , n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
L
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|