Increasing, decreasing, monotonic sequence

Sequences and limits

A sequence is increasing (or strictly increasing) if

a₁ < a₂ < . . . < a_n < a_n_{+
1} < . . . , or a_n_{+
1} > a_n for every n.

A sequence is decreasing (or strictly decreasing) if

a₁ > a₂ > . . . > a_n > a_n_{+
1} > . . . , or a_n_{+
1} < a_n for every n.

A sequence is called monotonic (monotone) if it is either increasing or decreasing.

Thus, increasing sequences either, diverge to + oo as n tends to infinity, written

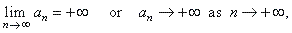(as, for example, the sequence of natural numbers) or it is bounded above, a_n < M for all n Î N, that is all terms of the sequence remain less than a fixed number M.

Decreasing sequences either, diverge to - oo as n tends to infinity, written

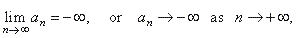(as, for example, the sequence -1, -2, -3, . . . ) or it is bounded below, a_n > m for all n Î N, that is all terms of the sequence remain greater than a fixed number m.

Monotonic sequence theorem

An increasing sequence, whose all terms are less than a fixed number M, tends to a finite limit value L that is not greater than M, therefore

if a_n_{+
1} > a_n and a_n < M, n = 1, 2, 3, . . . then

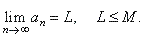A decreasing sequence, whose all terms are greater than a fixed number m, tends to a finite limit value L that is not less than m, therefore

if a_n_{+
1} < a_n and a_n > m, n = 1, 2, 3, . . . then

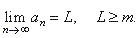Thus, every bounded monotonic sequence is convergent.

Example: Prove that the sequence given by

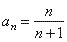is increasing and bounded.

Solution: Since

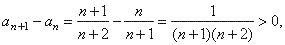that is, a_n_{+
1} > a_n for any natural number n, therefore the sequence is increasing.

By drawing the first few terms of the sequence on the number line and examining the n^th term expression as n tends to infinity, it follows that given sequence is bounded above by 1,

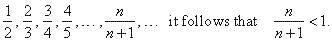Let verify that 1 is the limit of the sequence using the definition,

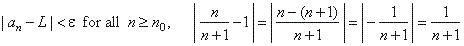therefore, as we can make the distance between the nth term and 1 as small as we wish by choosing n large enough, given sequence is convergent.

Sandwich theorem (result) or squeeze rule

Suppose that {b_n} is a sequence whose terms are bounded above and below (squeezed between) by sequences {c_n} and {a_n} respectively, such that

a_n < b_n < c_n for all n and if a_n ® L and c_n ® L, then b_n ® L.

Least upper bound (or supremum, abbrev. lub, sup) and greatest lower bound (or infimum, abbrev. glb, inf)

Suppose {a_n} is a bounded increasing sequence of real numbers, then the least upper bound of the set { a_n: n Î N } is the limit of {a_n}, so we write L = sup a_n.

Proof: Suppose L = sup a_n then, for given e > 0 there exists an integer n₀ such that

a_n0 > L - e or L - a_n0 < e.

Since {a_n} is increasing a_n > a_n0 > L - e for all n > n₀, and since L is the upper bound of the sequence then, L > a_n for every n, therefore

| L - a_n | = L - a_n < L - a_n0 < e for all n > n₀ that is, a_n ® L.

Similarly, if {a_n} is a bounded decreasing sequence of real numbers, then the greatest lower bound of the set { a_n: n Î N } is the limit of {a_n}, and we write L = inf a_n.

Contents H