44
 
Trigonometry
 Trigonometric functions
  Unit of measurement of angles - a radian (the circular measure)
 The central angle subtended by the arc equal in length to the radius, i.e. l = r,
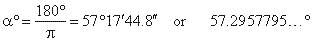we call it radian.
Thus, the angle a = 1° equals in radians,
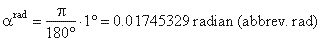or arc1° = 0.01745329. Arc is abbreviation from Latin arcus, (p = 3.1415926535... rad).
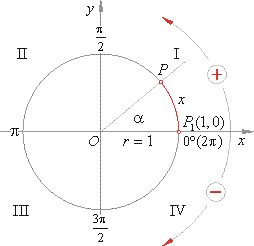
 The unit circle or trigonometric circle

A circle of radius r = 1, with the center at the origin O(0, 0) of a coordinate system, we call the unit or trigonometric circle, see the figure below.

The arc of the unit circle that describes a point traveling anticlockwise (by convention, clockwise is taken to be negative direction) from the initial position P1(1, 0) on the x-axis, along the circumference, to the terminal position P equals the angular measure/distance x = arad, in radians.

An angle is in standard position if its initial side lies along the positive x-axis.

If we take the positive direction of the x-axis as the beginning of a measurement of an angle (i.e., a = 0rad, both sides of an angle lie on the x-axis), and the unit point P1 as the initial point of measuring the arc, then the terminal side of an angle, which passes through the terminal point P of the arc, rotating around the origin (in any direction) describes different angles, and the terminal point P corresponding arcs,
x = arad + k · 2p,  k = 0, ±1, ±2, ±3, . . . 
or   x = a° + k · 360°,   k Î Z.
It means that every arc x ends in the same point P in which ends the corresponding arc a.

Thus, at any point P on the circumference of the unit circle end infinite arcs x = a + k · 2p, which differ by the multiplier 2p, and any number x associates only one point P.
 Division of the circumference of the unit circle to the characteristic angles
There is a common division of the circumference of the unit circle to the characteristic angles or the corresponding arcs which are the multipliers of the angles, 30° (p/ 6) and 45° (p/ 4).
 Definitions of trigonometric functions
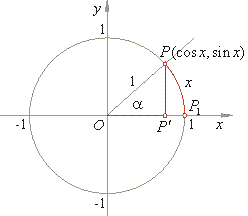
Let x be an arc of the unit circle measured counterclockwise from the x-axis. It is at the same time the circular measure of the subtended central angle a as is shown in the below figure.
In accordance with the definitions of trigonometric functions in a right-angled triangle,
 - the sine of an angle a (sina) in a right triangle is the ratio of the side opposite the angle to the hypotenuse.
 - the cosine of an angle a (cosa) in a right triangle is the ratio of the side adjacent to it to the hypotenuse.
Thus, from the right triangle OP′P, follows
sinx = PP′    The sine of arc x is the ordinate of the arc 
                    endpoint.
cosx = OP′  The cosine of arc x is the abscissa of the
                    arc endpoint.
The tangent of an angle a (tana) in a right triangle is the ratio of the lengths of the opposite to the adjacent side.
The cotangent is defined as reciprocal of the tangent, thus
From the similarity of the triangles OP′P and OP1S1,
Hence, the definition of the tangent function in the unit circle,
tanx = P1S1    The tangent of an arc x is the ordinate of intersection of the second or terminal side (or its
                      extension) of the given angle and the tangent line x = 1.
cotx = P2S2    The cotangent of an arc x is the abscissa of intersection of the second or terminal side (or 
                       its extension) of the given angle and the tangent y = 1.

It is obvious from the definitions that the tangent function is not defined for arguments x for which               cos x = 0, as well as the cotangent function is not defined for the arguments for which sin x = 0.
 Periodicity of trigonometric functions

Functions which have the characteristic to take the same values while their argument changes for all integral multiples of a constant interval (or a constant increases in amount called increment) we call periodic functions, and this constant interval we call period.
Hence, we say that trigonometric functions are periodic functions of x, so that
                            f (x) = sin x    and    f (x) = cos x   of the period  P = 2p,
while functions,      f (x) = tan x    and    f (x) = cot x   of the period  P = p.
The periodicity of trigonometric functions show the identities,
sin (a + k · 2p) = sin a    and    cos (a + k · 2p) = cos a,   k Î Z

                          tan (a + k · p) = tan a     and    cot (a + k · p) = cot a,   k Î Z
The table of signs of trigonometric functions
 Trigonometric functions of negative arcs or angles
 We say that arcs x and x′ are opposite if
x + x′ = 0  or  x′ = -x.
 Therefore,
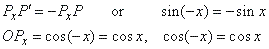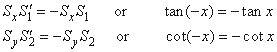Trigonometric functions of complementary angles Trigonometric functions of supplementary angles
    sin (p - x) = sin x,    tan (p - x) = - tan x
   cos (p - x) = - cos x,    cot (p - x) = - cot x
Trigonometric functions of arcs that differ on p/2 Trigonometric functions of arcs that differ on p
sin (p/2 + x) = cos x, tan (p/2 + x) = - cot x
cos (p/2 + x) = - sin x, cot (p/2 + x) = - tan x
    sin (p + x) = - sin x, tan (p + x) = tan x    
   cos (p + x) = - cos x,    cot (p + x) = cot x
  Trigonometric functions of arcs whose sum is 2p
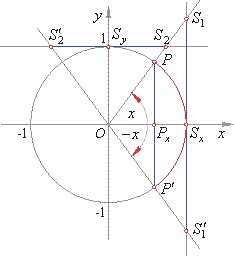
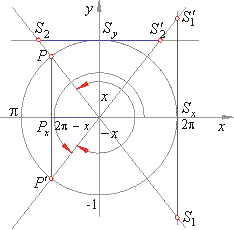
 The right figure shows relations between sides of the congruent right-angled triangles as follows, 
PxP′ =  - PxP      =>  sin (2p - x) = - sin x
  OPx = cos (2p - x),    cos (2p - x) = cos x
SxS1′ = -S xS1     =>    tan (2p - x) = - tan x
SyS2′ = - SyS2     =>    cot (2p - x) = - cot x
 
 
 
 
 
 
 
Contents E
 
 
 
 
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.