Oblique prism, Oblique pyramid, Volume and surface area of solids of revolution, Guldin’s rules, Applications of trigonometry in geodesy (or plane surveying), Applications of trigonometry in physics, using trigonometry in optics

Geometry and use of trigonometry

Applications of trigonometry in solid geometry

Oblique prism

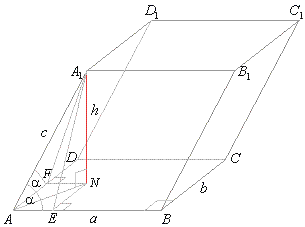
As an example of an oblique prism consider a parallelepiped whose lengths of the base edges and the lateral edges sharing a common vertex are, a, b and c. Edges, a and b of bases, are perpendicular to each other, while the lateral edge c, forms the angle a with each of them, see the figure below.

Determine the volume, the surface area of the parallelepiped and the angle lateral edge to base.

The volume V = B · h = a · b · h.

The altitude of the parallelepiped is the intersection line of the planes, A₁EN and A₁FN which are perpendicular to the base edges, a and b and thus to the plane of base.

Created triangles A₁AE and A₁AF are congruent as they share the hypotenuse and both have the same angle a.

Thus, A₁E = A₁F and therefore triangles, A₁EN

and A₁FN are congruent, so that EN = FN. AN is the bisector of the right angle DAB.

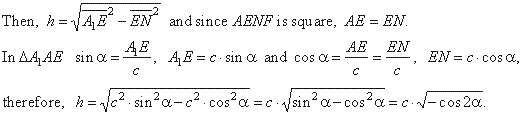As by hypothesis, the base edges at the vertex A are perpendicular and the lateral edge c forms equal angles a with the base edges, then must be a > 45°, or 2a > 90°, and therefore, - cos2a > 0.

Note that, if we follow changes (decrease) of the angle a while the height h tends to zero, finally, the end points A₁ and N will coincide, and the lateral edge c equals its orthogonal projection AN (bisector of the right angle, 2a = 90°).

So the volume of the parallelepiped

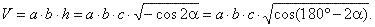Surface area S = 2B + S_lat. = 2ab + 2ac · sina + 2bc · sina = 2 · [ab + c · (a + b) · sina].

Inclination of the lateral edge to base,

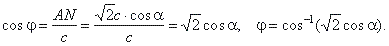Oblique pyramid

As an example we consider the pyramid with square base. Two opposite faces are isosceles triangles one of which forms with the base interior angle b, and the other forms with the plane of the base an exterior angle a. The height of the pyramid is h.

Determine the volume of the pyramid and angles that form two other lateral faces with the plane of the base.

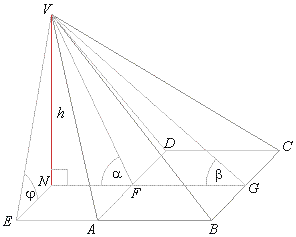
The plane VFG (F and G are midpoints of sides of base) is perpendicular to the plane of the base and passes through the height h of the pyramid.

Since a is an exterior angle of the triangle VFG, the foot N of the altitude h falls at the extension of the side FG.

The volume of the pyramid

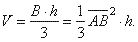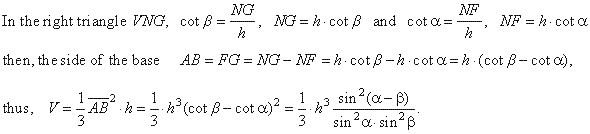The angle of inclination of the lateral sides VAB and VCD to the base we determine from the triangle VEN which is perpendicular to the plane of base, and whose leg is parallel with the edge AD of the base,

thus

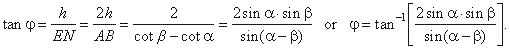Example: Bases of a triangular prism are isosceles triangles, ABC and A₁B₁C₁, with equal sides AB = AC and two equal angles a. The normal projection of the vertex of the upper base falls at the center of incircle of the radius r of the lower base. Through the base edge AC and the vertex B₁ laid is a plane inclined to the lower base at angle a. See the figure below.

Determine the surface area of the pyramid ABCB₁ cut off from the prism and the volume of the prism.

Solution: The section plane ACB₁ cut off from the prism the pyramid ABCB₁ the foot of the height of which is at the center O of incircle, so that all lateral faces are inclined to the base at equal angles a.

Therefore, we use the following formula for the surface area

Volume and surface area of solids of revolution, Guldin’s rules

For example, a regular hexagon of the side a rotates around an axe which passes through one of its sides, determine the surface area and the volume of generated solid of revolution.

The surface area equals to the lateral surface of a cylinder and lateral surfaces of two conical frustums, and lateral surfaces of two conics. Therefore,

Volume of the solid of revolution equals to the volume of the cylinder plus volumes of two conical frustums minus volume of two conics, that is

The same result can be obtained applying Guldin’s rules that states,

1) Surface area of a solid generated by rotation of a plane curve (a geometric figure) around an axe, which lies in the same plane but which do not intersect, equals to the product of the lengths of the curve (the figure’s perimeter) and the perimeter of the circle described by the centroid of the curve

(the centroid of the figure) therefore, S = P · P_G = P · 2p · r_G

Thus, applied to the preceding example, the centroid of the regular hexagon coincides with its center so, the perimeter of the circle described by the centroid,

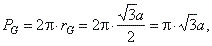and the perimeter of the regular hexagon P = 6a, plugging into above formula gives

S = P · 2p · r_G = 6a · Ö3pa = 6Ö3p · a².

2) Volume of a solid of revolution generated by the rotation of a figure around an axe which lies in the same plane as the figure, but which do not intersect, is equal to the product of the area of the figure and the perimeter of the circle described by the centroid of the figure,

therefore, V = A · P_G = A · 2p · r_G

Thus, for the volume of the solid of revolution from the preceding example

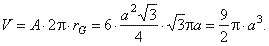Applications of trigonometry in geodesy (or plane surveying)

In plane surveying of geographical features, boundaries and areas are determined by the measurement of points and lines of direction on the earth's surface. Obtained horizontal and vertical distances and angles are then processed using computations based on geometry and trigonometry.

For example, to determine distance x between points, C and D, which cannot be measured directly, measured is the distance d between accessible points A and B and angles a₁, a₂ and b₁, b₂, as shown in the figure.

In D ABC,

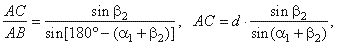and in D ABD,

applying the cosine law in the triangle ACD,

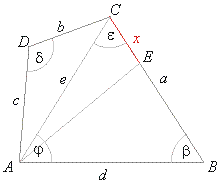
Example: A ground in form of a quadrilateral should be divided into two equal areas, see the below figure. At what distance from the vertex C dividing line segment AE intersects the side BC if lengths of sides are, b = 24 m, c = 28 m and d = 45 m, and angles b = 57° and d = 115°.

Solution: In DACD, e² = b² + c² - 2bc · cosd, e = 43.9 m,

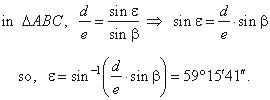since b + e + j = 180°, j = 180° - (e + b) = 63°44′19″.

The area of the quadrilateral ABCD as the sum of triangles ACD and ABC,

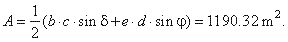The area of the triangle ABE is required to be half of the area of the quadrilateral, thus

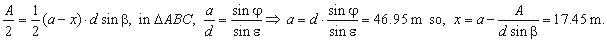Applications of trigonometry in physics

Physical laws, as results and available experimental data we explain and write applying mathematics methods. We can show that trigonometry is often used in these methods.

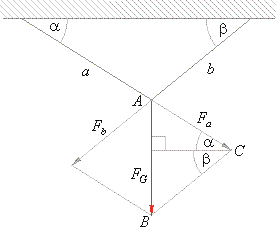
Take for example construction shown in the below figure that is loaded by a force F_G.

Determine the forces which act in the cable a and b that make the angle a and b with horizontal, respectively.

Resolve the resultant force F_G to its components F_a and F_b by using the parallelogram method on the vector diagram, thus in DABC

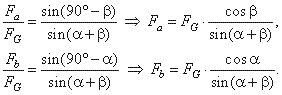An example of using trigonometry in optics

Two parallel light rays enter at an angle a to the normal of the surface of a triangular glass prism and pass through the prism. The paths of the rays (red) are shown in diagram below, taking into account the index of refraction for glass n = 1.5.

a) At what angle (denoted as g) upper ray exits the prism?

b) Find the declination d of the lower ray while exits the prism expressed in terms of the height h of the incidence and the side a of the prism.

Solution: Index of refraction

a) g = a - b + a₁ - b₁, b + b₁ = 60° => b₁ = 60° - b,

g = a - b + a₁ - 60° + b = a + a₁ - 60° = a₁ - 30°,

Note that triangles, AEC and EBD are similar as their corresponding angles are equal.

Contents E