|
|
|
|
Analytic geometry
- Conic sections
|
|
|
|
Hyperbola
and line
|
|
Hyperbola and line relationships
|
|
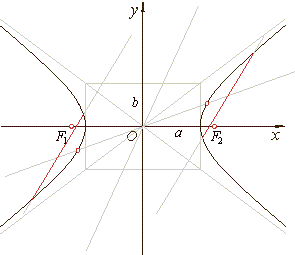
Let examine relationships between a hyperbola and a line passing through the center of the hyperbola, i.e., the
origin. A line y =
mx intersects the hyperbola at two
points if
the slope
|
|
|m|
<
b/a but
if |m|
> b/a
then,
the line
|
|
y =
mx does not intersect the hyperbola at all.
|
|
The diameters of a hyperbola are straight lines
passing through its center.
|
|
The asymptotes divide these two pencils of diameters
into, one which intersects the curve at two points, and
the
other which do not intersect.
|
|
A diameter of a conic section is a line which passes
through the midpoints of parallel chords.
|
|
Conjugate diameters of the hyperbola (or the ellipse) are two diameters such that each bisects all chords
drawn parallel to the other.
|
|
 |
|
| As the equation of a hyperbola can be obtained from the equation of an ellipse by changing the sign of
b2
|
|
that is, a2(1
-
e2)
= -a2(e2
-
1) =
-b2, |
|
this way, we can use other formulas relating to the ellipse to obtain corresponding
formulas for the hyperbola. Therefore, to examine conditions which determine position of a line in relation to a hyperbola
we
solve the system of
equations, |
|
y =
mx + c
then if,
a2m2
-
b2
> c2
the line intersects the hyperbola at two points,
|
|
b2x2
-
a2y2
= a2b2
a2m2
-
b2
< c2
the line and the hyperbola do not intersect. |
|
a2m2
-
b2 = c2
the line is the tangent of the hyperbola,
|
|
|
Condition for a line to be the tangent to the hyperbola -
tangency condition
|
| A
line is the tangent to the hyperbola if
a2m2
-
b2 = c2,
this equality is called the tangency
condition. |
|
Regarding
the asymptotes, to which c
= 0, this condition gives
|m|
= b/a
and that is why we can say that the hyperbola touches the asymptotes at infinity. |
| The tangency condition also
states that the slopes of the tangents
will satisfy the condition if |
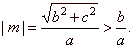 |
| That is, the tangents to the hyperbola can only be parallel to a line belonging to the pencil of lines that do not
intersects the hyperbola. |
|
|
The equation of the tangent at the point on the hyperbola
|
|
The points of contact of a line and the hyperbola can be obtained from the corresponding formula for the ellipse by changing
b2
with -b2
thus, |
|
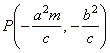 |
the
tangency point or the point of contact. |
|
| Thus,
the intercept and slope of the
tangent |
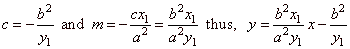 |
|
|
or b2x1x
-
a2y1y
= a2b2
the equation of the tangent at a point P1(x1,
y1)
on the hyperbola.
|
|
|
Polar and pole of the hyperbola
|
|
If from a point
A(x0, y0), exterior to the hyperbola, drawn are tangents, then the secant line passing
through the contact points, is the polar of the point A.
The point A
is called the pole of the polar. |
| The equation of the
polar is derived the same way as for the ellipse, |
| b2x0x
-
a2y0y
= a2b2
the equation of the
polar of the point A(x0, y0). |
|
|
Construction of the tangent at the point on the hyperbola
|
|
The tangent at the point
P1(x1,
y1)
on the hyperbola is the bisector of the angle F1P1F2
subtended by |
|
|
|
|
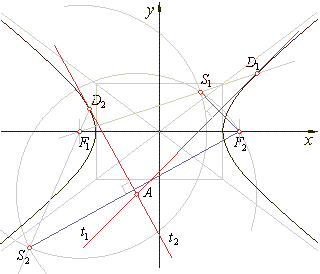
Construction of tangents from a point outside the hyperbola
|
|
With A as center draw an arc through
F2,
and from F1as center, draw an arc of radius
2a.
|
|
These arcs intersect at points
S1
and
S2.
|
|
Tangents are the
perpendicular bisectors of the line segments F2S1
and
F2S2.
|
|
Tangents can also be drawn as lines through
A and
the intersection points of lines through F1S1
and F1S2,
with the hyperbola.
|
|
These intersections are at the same
time the points of contact
D1
and
D2.
|
|
 |
|
|
Example:
The line 13x
-
15y
-
25 = 0 is the tangent of a hyperbola with linear eccentricity (half the focal
distance) cH =
Ö41.
Write the equation of the hyperbola.
|
|
Solution:
Rewrite the equation 13x
-
15y
-
25 = 0
or |
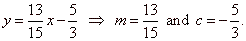 |
|
| Using
the linear eccentricity |
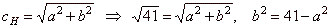 |
|
| and
the tangency condition |
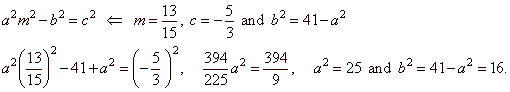 |
| hus,
the equation of the hyperbola, |
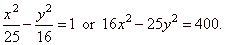 |
|
|
|
Example:
Find the normal to the hyperbola
3x2
-
4y2 = 12 which is parallel to the line
-
x +
y = 0.
|
|
Solution: Rewrite the equation of the hyperbola
|
| 3x2
-
4y2 = 12
| ¸12
|
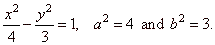 |
|
The slope of the normal is equal to the slope of
the given line,
|
| y =
x
=> m
= 1,
mt =
-1/mn,
so mt =
-1
|
|
applying the tangency condition
|
| a2m2
-
b2 = c2
<= mt =
-1,
a2 =
4,
b2 = 3
|
| 4·(-1)2
-
3 = c2
=> c1,2 = ±1
|
| tangents
t1
::
y =
-x
+ 1,
t2
::
y =
-x
-
1.
|
| The points of
tangency,
|
|
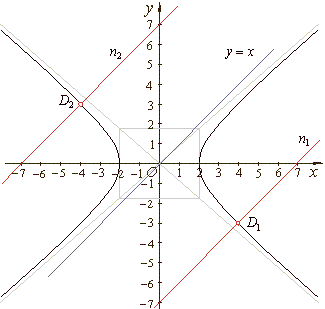 |
|
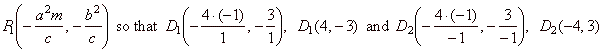 |
|
The
equations of the normals,
|
| D1(4,
-3)
and m =
1
=>
y -
y1 = m ·(x
-x1),
y +
3 = 1·(x
- 4)
or n1
::
y = x -
7, |
| D2(-4,
3)
and m =
1 =>
y -
y1 = m ·(x
-x1),
y -
3 = 1·(x
+ 4)
or n2
::
y =
x + 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
D
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|