|
|
|
|
Analytic geometry
- Conic sections
|
|
|
|
Equilateral or rectangular
hyperbola
|
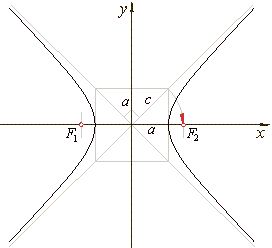
| The hyperbola whose semi-axes are equal, |
| i.e.,
a
= b,
has the equation
x2 -
y2
= a2. |
|
Its asymptotes
y
=
± x
are perpendicular and inclined to the x-axis at an angle of
45°. |
| Foci of the equilateral hyperbola,
|
| F1(-Ö2
a,
0) and
F2(Ö2
a,
0),
|
|
and the eccentricity,
e
= c/a
= Ö2.
|
|
 |
|
|
|
Translated hyperbola
|
|
The equation of a hyperbola translated from standard position so that its center is at
S(x0, y0)
is given by
|
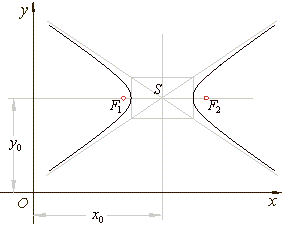
| b2(x
-
x0)2
-
a2(y
-
y0)2
= a2b2 |
| or |
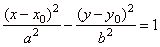 |
|
| and after expanding and substituting constants
obtained is
|
| Ax2
+ By2
+ Cx + Dy + F
= 0.
|
|
An equation of that form represents the hyperbola if
|
|
A · B < 0
|
| that is, if coefficients of the square terms have
different signs.
|
|
 |
|
|
|
Equation of the hyperbola in vertex form
|
|
By translating the hyperbola, centered at
(0, 0), in the negative direction of the x-axis by
x0
= - a,
|
| so that new
position of the center S
(- a, 0)
then its |
|
equation is
b2(x
+ a)2
-
a2y2
= a2b2. |
|
After squaring and reducing,
|
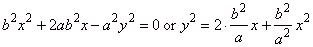
|

|
|
the equation of the hyperbola in vertex form.
|
|
 |
|
|
|
Parametric equation of the hyperbola
|
|
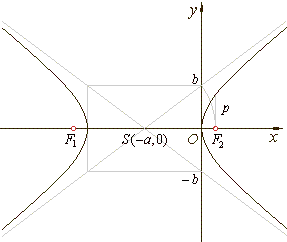
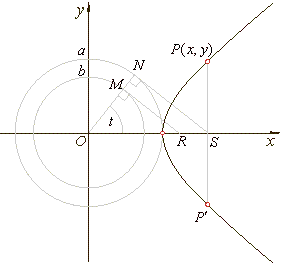
In the construction of the hyperbola, shown in
the below figure, circles of radii
a
and b
are intersected by an arbitrary line through the origin at points M
and N. Tangents to the circles at
M
and N
intersect the x-axis at
R
and S.
On the perpendicular through S, to the
x-axis, mark the line segment
SP of length
MR to get the point
P of the hyperbola.
We can prove that P is a point of the hyperbola.
|
| In the right
triangles ONS and
OMR,
|
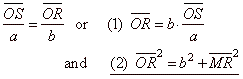 |
| by replacing OS
= x
and MR
= SP
|
|
and substituting |
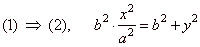 |
|
| by
dividing by b2, |
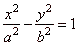 |
|
|
therefore, P(x, y)
is
the point of the hyperbola.
|
|
 |
|
The coordinates of the point
P(x, y)
can also be expressed by the angle t
common to both mentioned
|
| triangles,
so that |
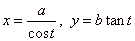 |
is the parametric equation of the hyperbola. |
|
|
By substituting these parametrically expressed coordinates into equation of the hyperbola
|
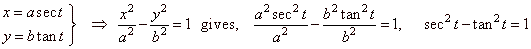
|
| that
is, |
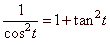 |
known
trigonometric identity. |
|
|
|
|
Example:
The hyperbola is given by equation
4x2
-
9y2 + 32x + 54y -
53 =
0. Find coordinates of the
center, the foci, the eccentricity and the asymptotes of the hyperbola.
|
|
Solution: The given hyperbola is translated in the direction of the coordinate axes so the values of
translations x0 and
y0
we can find by using the method of completing the square
rewriting the equation in |
| the standard
form, |
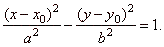 |
|
|
Thus,
4x2 + 32x
-
9y2 + 54y -
53 =
0,
|
| 4(x2 + 8x) -
9(y2 -
6y) -
53 =
0
|
|
4[(x +
4)2 -
16] -
9[(y -
3)2 -
9] -
53 =
0
|
|
4(x + 4)2 -
9(y -
3)2 = 36 | ¸
36
|
| Therefore,
|
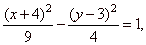 |
|
|
 |
|
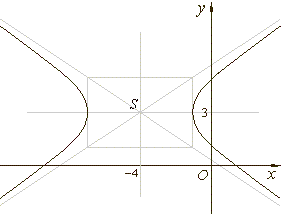
| it
follows that a2 =
9, a
= 3, b2 = 4,
b
= 2, and the center of the hyperbola at
S(x0, y0)
or S(-4,
3). |
| Half
the focal distance |
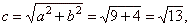 |
the
eccentricity |
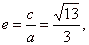 |
|
|
and the foci, F1(x0
-
c,
0) so
F1(-4
-
Ö13,
0) and
F2(x0
+ c,
0),
F1(-4
+ Ö13,
0). |
| Equations of the asymptotes of a translated hyperbola |
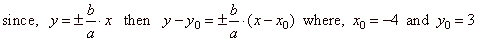 |
| therefore, the asymptotes of the given
hyperbola, |
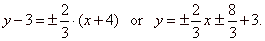 |
|
|
|
Example:
Write the equation of the hyperbola 9x2
-
25y2 = 225
in the vertex form.
|
|
Solution: Using
parallel shifting we should place the center
of the hyperbola at S(-a,
0). |
| Rewrite
9x2
-
25y2 = 225 | ¸
225 |
|
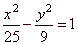 |
therefore,
a = 5 and
b = 3,
so that S(-5,
0). |
|
| Then, the translated
hyperbola with the center at S(-5,
0) has the equation
|
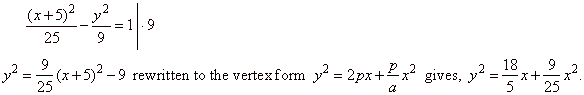 |
|
|
Equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
| The
graph of the reciprocal function |
| y
= 1/x or
y
= k/x |
| is a rectangular
(or right) hyperbola of which asymptotes are the coordinate axes. |
|
If k
> 0 then, the
function is decreasing from zero to negative infinity
and from positive infinity to zero, i.e., the graph of
the rectangular hyperbola opening in the first and third
quadrants as is shown in the right figure.
|
| The vertices, |
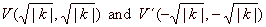 |
|
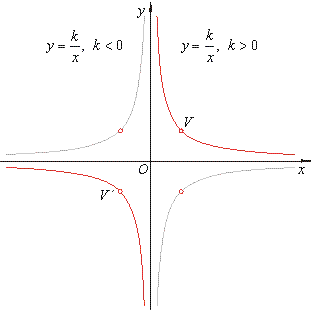 |
|
|
Translation
of equilateral or rectangular hyperbola with the coordinate axes as its
asymptote
|
| The
graph of the translated reciprocal function or
the linear rational
function |
| Translated
rectangular hyperbola we can
write as, |
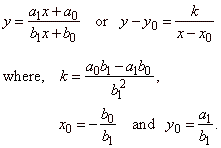 |
| The
k
is constant, x0
and y0
are horizontal and vertical
asymptotes respectively. Therefore,
the values of the vertical and the horizontal asymptotes correspond to
the coordinates of the |
|
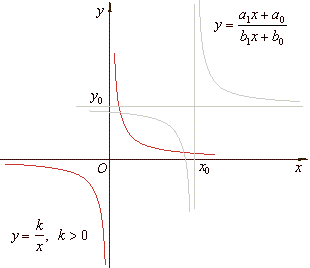 |
|
| horizontal and the vertical translation of the
reciprocal function y
= k/x as is shown in
the above figure. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
D
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|