7
 
ALGEBRA
Systems of linear equations
 :: Cramer’s rule, using the determinant to solve systems of linear equations
Solving system of two equations in two unknowns using Cramer's rule

  A system of two equations in two unknowns, the solution to a system by Cramer’s rule (use of determinants).

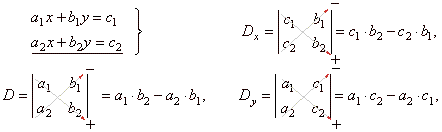the solution to the system
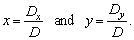Example:  Solve given system of linear equations using Cramer’s rule.
Solving system of three equations in three unknowns using Cramer's rule
 

A determinant of rank n can be evaluated by expanding to its cofactors of rank n - 1, along any row or column taking into account the scheme of the signs.

Example:   The determinant of rank n = 3,
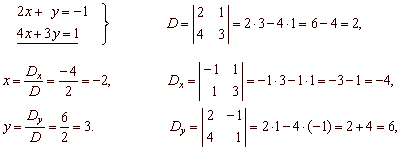Method of expanding a determinant of a rank n by cofactors, example

Property of a determinant: The value of a determinant will not change by adding multiples of any column or row to any other column or row. This way created are zero entries that simplify subsequent calculations.

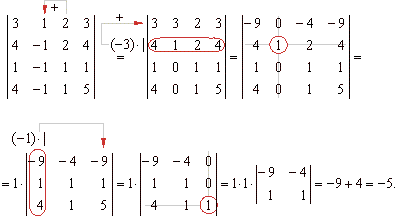
Example:  An application of the method of expanding a determinant to cofactors to evaluate the determinant of the rank four.

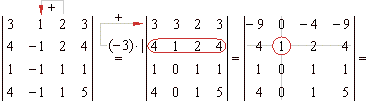Added is third to the second colon. Then, the second row multiplied by -3 is added to the first row. The obtained determinant is then expanded to its cofactors along the second colon:

The first colon multiplied by -1 is added to the third colon. The obtained determinant is then expanded along the third colon.

 Absolute value equations
 ::  Solving absolute value equations

To solve an absolute value equation, isolate the absolute value on one side of the equation, and use the definition of absolute value.

The absolute value of a real number a, denoted | a |, is the number without its sign and represents the distance between 0 (the origin) and that number on the real number line.

Thus, regardless of the value of a number a its absolute value is always either positive or zero, never negative that is,  | a | > 0.

Example:     | 1 - 2x | = 17
Solution:        1 - 2x = 17                             or                      1 - 2 x = - 17
                         2 x = - 16                                                          2x = 18
                            x = - 8                                                              x = 9
The solutions to the given equation are x = - 8 and x = 9.
Example:     | x + 2 | = | 2x - 5 |

Solution:   As both sides of the equation contain absolute values the only way the two sides are equal is, the two quantities inside the absolute value bars are equal or equal but with opposite signs.

                      x + 2 = 2x - 5                             or                      x + 2 = - (2 x - 5)
                     x - 2x = - 5 - 2                                                     x + 2 = - 2 x + 5
                            -x = - 7                                                                 3x = 3
                              x = 7                                                                     x = 1
Check solutions:      x = 7   =>    | x + 2 | = | 2x - 5 |,            x = 1   =>    | x + 2 | = | 2x - 5 |
                                                  | 7 + 2 | = | 2 · 7 - 5 |                              | 1 + 2 | = | 2 · 1 - 5 |
                                                            9 = 9                                                      3 = | -3 |
Therefore, the solutions to the given equation are  x = 7 and  x = 1.
 Inequalities
 :: Linear inequality

Solving inequalities:  The solutions to an inequality are all values of x that make the inequality true. Usually the answer is a range of values of x that we plot on a number line.

Multiplying or dividing both sides of an inequality by the same negative number, the sense of the inequality changes, i.e., it reverses the direction of the inequality sign.

Example:     3(x - 2) > - 2(1- x)
Solution:        3x - 6 > -2 + 2x
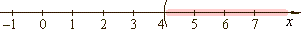                            x > 4 the interval notation (4, oo)

The open interval  (4, oo) contains all real numbers between given endpoints, where round parentheses indicate exclusion of endpoints.
Example:
Solution:    - 4x + 9 - 3x < 6 - 5 + 5x 
the interval notation
                             - 12x < - 8
                                  x > 2/3

The half-closed (or half-open) interval contains all real numbers between given endpoints, where the square bracket indicates inclusion of the endpoint 2/3 and round parenthesis indicates exclusion of infinity.

 :: Compound or double inequalities
Use the same procedure to solve a compound inequality as for solving single inequalities.
Example:      - 4 < 2(x - 3) < 5

Solution:  We want the x alone as middle term and only constants in the two outer terms. Remember, while simplifying given compound inequality, the operations that we apply to a middle term we should also do to the both left and right side of the inequality.

                    - 4 < 2(x - 3) < 5 | ¸ 2
                           
the interval notation
 
 
 
 
 
 
Contents A
 
 
 
 
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.