|
|
|
|
ALGEBRA
|
|
|
|
::
Rational
Inequalities
|
|
A rational inequality can be written
in one of the following standard forms:
|
|
P/Q > 0
or P/Q < 0
(or
P/Q > 0
or P/Q < 0), where
Q
is not 0.
|
|
The sign of the rational expression
|
|
P/Q, where
P
and Q
are polynomials, depends on the signs of P
and
Q.
|
|
Method of solving
rational inequalities
|
|
As the signs of the
polynomials change at the zeros, to solve a rational inequality we should find the zeros of
both P
and Q
first and then we can determine the intervals of the independent variable that satisfy given rational inequality.
|
|
By setting the numerator to
0 we get the zero points of the given rational expression, but by setting the denominator
to 0 we get points at which the rational expression or function is undefined
(i.e., when plugged into the expression give division by zero).
|
|
|
Example: |
Solve the rational
inequality
|
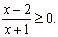 |
|
|
Solution:
The solution set of the given rational inequality includes all numbers
x
which make the inequality greater then or equal to 0, or which make the sign of the rational expression
to be positive or 0.
|
|
A rational expression is positive if both the numerator and the denominator are positive
or if both are negative, and the rational expression equals 0 when
its numerator is equal to 0. Therefore, we have to solve the two simultaneous
inequalities
|
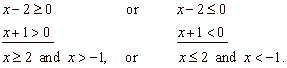
|
|
The solutions represented on the
number line are shown below.
|

|
|
Thus, the solution set of the given
inequality written in the interval notation is (-
oo,
-1)
U
[2, oo ).
|
|
|
Example: |
Find the solutions
of the inequality
|
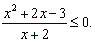 |
|
|
Solution:
The solution set of the given rational inequality includes all numbers
x
which make the inequality less then or equal to 0, or which make the sign of the rational expression
to be negative or 0.
|
|
A rational expression is negative if the numerator and the denominator
have different signs, and the rational expression equals 0 when
its numerator is equal to 0 that is, we have to solve two simultaneous
inequalities.
|
|
We graph the numerator and the
denominator in the same coordinate system to find all points of
the x-axis
that satisfy given inequality.
|
|
The zero points of the numerator and
the denominator divide the x-axis
into four intervals at which given rational expression changes
sign.
|
|
|
|
The solutions of the two pairs of the simultaneous
inequalities are intersections of sets of their partial solutions,
|
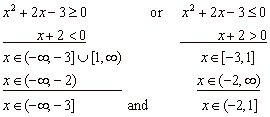
|
|
as is shown below.
|
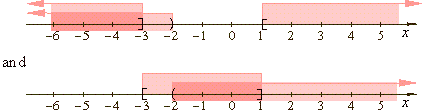
|
|
Therefore, the solution set is (-
oo, -3]
U
(-2,
1].
|
|
|
|
::
Absolute value
inequalities
|
|
Graphical
interpretation of the
definition of the
absolute value of a function y =
f
(x) will help us solve
linear inequality with absolute value. The
definition for the absolute value of a function is given by
|
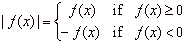
|
|
Solving
linear inequalities with absolute value
|
|
Thus,
for
values of x
for which f
(x)
is nonnegative, the graph of | f
(x)| is the
same as that of f
(x).
|
|
For values of
x
for which f (x)
is
negative, the graph of | f
(x)
| is a reflection of
the graph of f (x)
on the x-axis.
That
is, the
graph of y = -
f
(x) is obtained by reflecting the graph
of y = f
(x)
across the x-axis.
|
|
|
|
|
::
Systems
of linear inequalities
|
|
Solving and graphing systems of
linear inequalities
|
|
The solution of the system of
simultaneous inequalities is the intersection of sets
of individual solutions.
|
|
|
Example: |
Solve and graph the
solution of the given system of simultaneous inequalities.
|
|
|
|
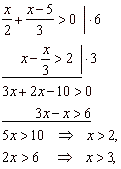 |
|
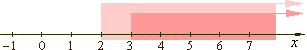 |
|
| the solution of the system
is the open interval (3, +
oo ). |
|
|
|
|
|
|
::
Systems of
linear inequalities in two variables
|
|
Solving and graphing
systems of
linear inequalities in two variables
|
|
The set of points whose coordinates (x,
y)
satisfy the inequality ax+
by + c > 0 is a
half-plane of a Cartesian plane.
|
|
|
Example: |
Solve and graph the
solution of the given system of linear inequalities in two
variables.
|
|
|
|
| Plug the
coordinates of the origin |
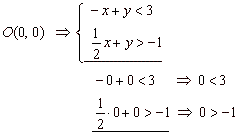 |
|
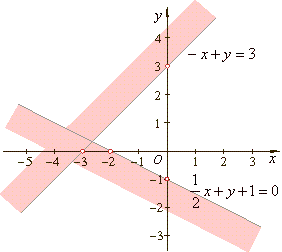 |
|
|
|
|
::
Quadratic
inequalities
|
|
To solve a quadratic inequality we
examine signs of the
equivalent quadratic function.
|
|
The
x-intercepts
or roots are the points where a quadratic function changes the sign. The
x-intercepts determine
the three intervals on the x-axis in which the function is above or
under the x-axis, that is, where the function is positive or negative.
|
|
Graphic solution of
quadratic inequalities
|
|
|
Example: |
Solve the inequality
-
x2
+ 2x
+
3 ≤
0.
|
|
|
Solution:
Solve the quadratic
equation ax2
+ bx
+
c
= 0
to get the boundary points.
|
|
The zeroes
or roots of equivalent function (see the graph
below) are the endpoints of the intervals and are included in the solution.
|
|
The turning point V(x0,
y0),
V(1,
4) |
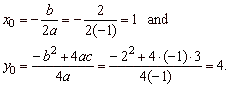 |
|
The roots of, -
x2
+ 2x
+
3 =
0 |
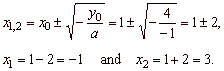 |
|
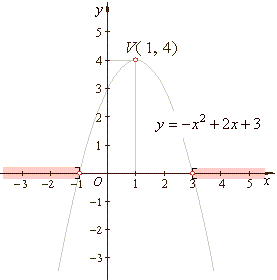 |
| Solution: |
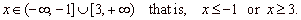 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents A
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|