|
| Trigonometry |
|
|
|
|
 Calculation of values of trigonometric functions
Calculation of values of trigonometric functions
|
|
Trigonometric
reduction formulas - the reference angles |
|
Calculation of
values of trigonometric functions of an arbitrary angle x, examples |
|
|
|
|
|
|
| Calculation of values of trigonometric functions
|
| Trigonometric
reduction formulas - the reference angles |
|
Values of trigonometric functions, of any angle greater than
90° (p/2)
can be expressed by the corresponding value of the function of an angle from the first quadrant.
|
|
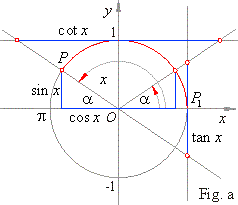
The figures, a, b and c below,
show these relations for the angles x
whose terminal side falls in the second, third or fourth quadrant.
|
|
The acute angle
a between the
x-axis and the terminal side of angle
x
we call the reference angle.
|
|
Angles x
whose terminal side falls in the second quadrant
|
|
we denote
as, x =
p
- a.
|
|
|
|
|
|
|
|
|
|
 |
|
|
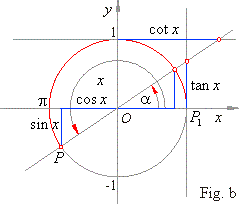
Angles x
whose terminal side falls in the third quadrant we denote
as, x =
p
+ a
|
|
Angles x
whose terminal side falls in the third quadrant
|
|
we denote
as, x =
p
+ a.
|
|
|
|
|
|
|
|
|
|
 |
|
|
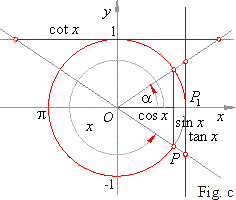
Angles x
whose terminal side falls in the fourth quadrant
|
|
we denote
as, x =
2p
- a.
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
If a given arc x
is greater than
2p then, before calculating values of
functions sine and cosine, we should divide it by
2p,
while for functions tangent and cotangent by
p, to determine integral multiplier
k and reminder
a
therefore,
|
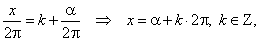
|
|
and for functions, tangent and cotangent
|
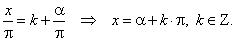
|
|
|
|
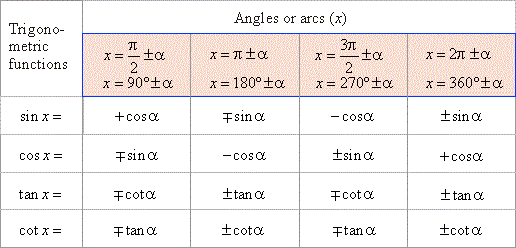
Given properties of trigonometric functions are included in the reduction formulas that give the value of
any angle
x
greater than 90° (p/2)
in terms of same function of an acute angle a.
|
|
|
We calculate values of trigonometric functions of an arbitrary angle
x
by using its reference angle
a.
|
|
If x
is an angle in standard position, then its reference angle is given by the acute angle
x
which is enclosed between the terminal side of the
x
and the
x-axis.
|
|
|
|
|
|
Calculation of values of trigonometric functions of an arbitrary angle
x examples
|
| Example:
Calculate sin
1110°.
|
|
Solution:
To use the expression x =
a +
k · 360° we should divide given angle by
360°
to get an integer multiple k and remaining angle
a,
thus
|
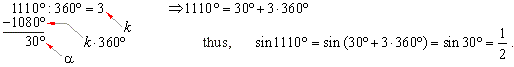
|
|
|
| Example:
Calculate cos
(-
77p/4).
|
|
Solution:
Since cos
(-
x) = cos x
we can write cos
(-
77p/4)
= cos 77p/4,
|
|
then, divide given x
by
2p,
x = 77p/4
= 19p
+ p/4
= 9 · 2p
+ 5p/4
|
|
so that, cos
(-
77p/4)
= cos 77p/4
= cos (9 · 2p
+ 5p/4)
= cos 5p/4.
|
|
As the terminal side of the angle 5p/4
lies in the third quadrant we use cos
(p
+ a) = -
cos a
|
|
therefore, cos
5p/4
= cos
(p
+ p/4) =
-
cos p/4
= -
Ö2/2.
|
|
|
| Example:
Calculate tan
817° 35′ 42″.
|
|
Solution:
According to x =
a +
k · 180°
we divide the given angle x
by 180° to
determine k
and a,
so
|
|
x = 817° 35′ 42″ = 97° 35′ 42″ + 4 · 180°
|
|
thus, tan
817° 35′ 42″ = tan (97° 35′ 42″ + 4 · 180°) = tan 97° 35′ 42″,
|
|
as it is second-quadrant angle we use tan
(180° -
a) = -
tan
a
|
|
that is, 180° -
a =
179° 59′ 60″ -
97° 35′ 42″ = 82° 24′ 18″
|
|
therefore, tan
97° 35′ 42″ = tan (180° -
82° 24′ 18″) = -
tan 82° 24′ 18″ =
-
7.49964.
|
|
When we use a scientific calculator to find values for trigonometric functions, a given angle should be entered as decimal degree in DEG mode, so input
|
|
82.2418
INV ®DEG
=> 82.405° TAN
=>
7.49964367.
|
|
|
| Example:
Calculate cot
27p/7.
|
|
Solution: Decompose the angle to
x =
a +
k · p,
that is, x =
27p/7 =
(3 + 6/7)p =
6p/7
+ 3p thus,
|
|
cot
27p/7 =
cot (6p/7
+ 3p) =
cot 6p/7
since for a fourth-quadrant angle
holds cot
(2p
-
a) = -
cot
a
|
|
then, cot
6p/7 =
cot (2p
-
p/7)
= -
cot
p/7 =
-
2.07652.
|
|
When we use calculator we set it in
the RAD mode using DRG key, then enter,
|
|
INV p
¸
7 =
0.44879895 TAN
(0.481574618) 1 / x
=>
2.076521397.
|
|
That is, the value of the function cotangent we calculate as the reciprocal value of the function
tangent, as
|
|
cot x = 1/tan x.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Trigonometry
contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |