|
| Trigonometry |
|
|
|
|
 Trigonometric
functions of arcs from 0
to ±
2p
Trigonometric
functions of arcs from 0
to ±
2p
|
 Values of
trigonometric functions of arcs p/6, p/4 and p/3
Values of
trigonometric functions of arcs p/6, p/4 and p/3 |
|
The values of the trigonometric functions of arcs that are multipliers of
30°
(p/6)
and 45°
(p/4) |
|
|
|
|
|
|
|
|
|
Values of
trigonometric functions of arcs
p/6, p/4
and
p/3
|
|
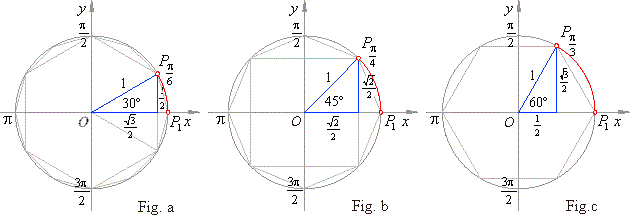
The given arcs are, one twelfth, one eighth and one sixth of the circumference
2p
of the unit circle so the coordinates of terminal points of the arcs are the elements of the equilateral triangle with the side
a = 1
(Fig.a, c) and the sides of the square with diagonal
d = 1, (Fig.
b).
|
|
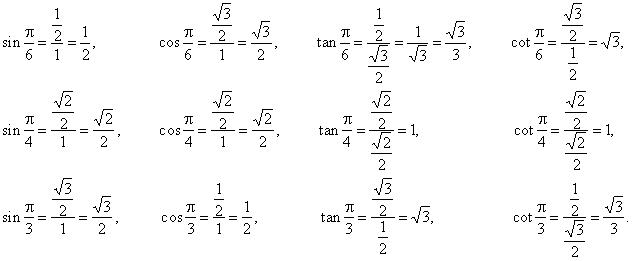
|
|
|
|
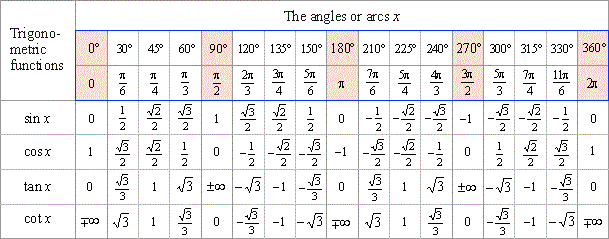
The values of the trigonometric functions of arcs that are multipliers of
30°
(p/6)
and 45°
(p/4)
|
|
|
|
| Example:
Calculate, sin
3p/2
· cos (-
p)
+ tan 5p/4.
|
| Solution: sin
3p/2
· cos (-
p)
+ tan 5p/4
= -
1 · (-
1) + tan (p
+ p/4)
= 1 + tan p/4
= 1 + 1 = 2. |
|
|
| Example:
Calculate, |
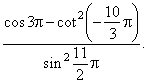 |
|
|
Solution:
|
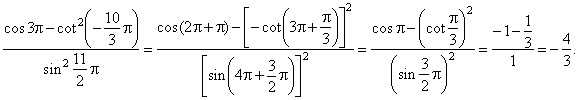
|
|
|
|
Example:
Prove the identity,
|
|
cos2 p/3
· sin (p/2
-
x) -
cos (p
-
x)
· cos2 p/6
= tan (p/2 +
x)
· sin (2p
-
x).
|
|
Solution:
Since sin
(p/2
-
x) = cos
x,
cos (p
-
x) = -
cos
x, tan (p/2 +
x) = -
cot
x
|
|
and sin
(2p
-
x) = -
sin x
then,
|
|
(cos p/3)2
· cos
x -
(-
cos
x)
· (cos p/6)2
= -
cot
x
· (-
sin x),
|
|
(1/2)2
· cos
x + (Ö3/2)2
· cos
x = (cos
x/sin x)
· sin x
=> cos
x = cos
x.
|
|
|
|
Example:
Prove the identity,
|
|
cot2 (p +
x)
· cos2 (p/2 +
x) + sin (-
x) · sin (p +
x) = tan (2p
-
x) · cot (-
x).
|
|
Solution:
[cot (p +
x)]2
· [cos (p/2 +
x)]2 +
(-
sin x)
· sin (p +
x) = (-
tan x)
· (-
cot x),
|
|
(cot
x)2
· (-
sin x)2
+ (-
sin x) · (-
sin x) = (sin x/cos
x)
· (cos
x/sin x)
|
|
cos2
x + sin2
x = (sin x/cos
x)
· (cos
x/sin x) = 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Trigonometry
contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |