|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
Polynomial and/or
polynomial functions and equations |
|
Quadratic
equations with absolute value
|
|
|
|
|
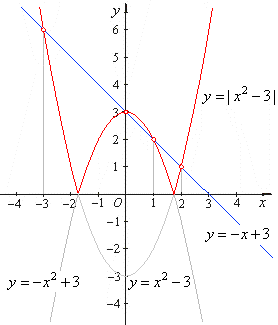
Solve the absolute value
equation
| x2
-
3 | =
-
x + 3.
|
|
|
Solution:
Using the definition of the
absolute value of a function we can write,
|
| if
x2
-
3 > 0
then |
x2 -
3 | =
x2 -
3, |
| and
given equation x2
-
3 =
-
x + 3
or |
|
x2
+ x -
6 =
0.
By
factoring the equation, |
|
x2 +
3x
-
2
x -
6 =
[x(x + 3) -
2(x + 3)] |
|
x2
+ x -
6 =
(x + 3)(x -
2) =
0 |
| so,
x
+ 3 =
0,
x1
= -
3
and x
-
2 =
0,
x2
= 2. |
| If
x2
-
3 < 0
then |
x2 -
3 | =
-
(x2
-
3), |
| and
given equation -
(
x2 -
3) =
-
x + 3
or |
| -
x2
+
x =
x(-
x + 1) =
0 |
| so,
x3
= 0
and -
x + 1 =
0,
x4
= 1. |
|
 |
|
| Therefore,
the solutions of the given equation, x1
= -
3, x2
= 2,
x3
= 0
and x4
= 1 are the abscissas of the
intersection points of, y = |
x2 -
3 | and y = -
x + 3
functions, as shows the above figure. |
|
|
|
|
Solve the absolute value
equation
| 2x2
-
x -
3 | = -
x + 5.
|
|
| Solution:
Using the definition of the
absolute value of a function we can write, |
| if
2x2
-
x -
3 > 0 |
| then
|
2
x2
-
x -
3 | =
2
x2
-
x -
3, |
| and
given equation 2
x2
-
x -
3 =
-
x + 5 |
|
or 2x2
=
8,
x2
=
4, |
| so,
x1,2
= +
2,
x1
= -
2
and x2
= 2. |
| if
2
x2
-
x -
3 < 0 |
| then
|
2x2
-
x -
3 | =
-
(2x2
-
x -
3), |
| and
given equation -
(2
x2
-
x -
3) =
-
x + 5, |
|
-
2x2
+
2x
-
2
= 0
or x2
-
x + 1
= 0, |
 |
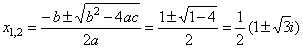| thus,
there are no real solutions in this case. |
|
 |
|
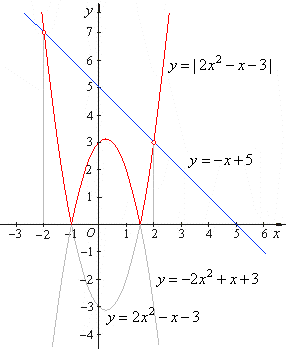| Therefore,
the solutions of the given equation, x1
= -
2 and x2
= 2 are the abscissas of the
intersection points of, y = |
2
x2
-
x -
3 | and y = -
x + 5
functions, as is shown in the above figure. |
|
|
|
Cubic
functions or the third degree polynomial
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
|
|
|
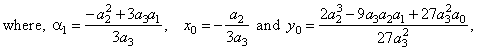
By
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
=
a3x3
+
a1x
where a1=
tan at
.
|
|
Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I(x0,
y0).
|
|
|
|
|
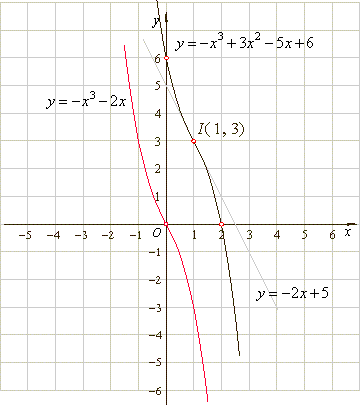
Find the coordinates of
translations, the zero point, the point of inflection and draw
graphs of
the
|
|
|
cubic function y
=
-
x3
+ 3x2
-
5x
+
6
and its source function.
|
|
Solution:
1)
Calculate the coordinates of translations
|
|
|
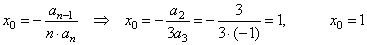
y0
= f(x0)
=> y0
= f (1)
=
-13
+ 3 · 12
-
5
· 1
+
6 =
3,
y0
= 3.
|
|
Therefore,
the point of inflection I(1,
3).
|
|
2)
To
get the source cubic function, plug the coordinates
of translations into the general
form
of the cubic,
|
|
y
+ y0
=
a3(x
+
x0)3
+ a2(x
+
x0)2
+ a1(x
+
x0)
+ a0
|
|
thus, y
+ 3
=
-1·
(x
+
1)3
+
3 · (x
+
1)2
-
5
· (x
+
1)
+
6 => y
=
-
x3 -
2x
the source
function.
|
|
Since given function is symmetric to its
point of inflection, and as the y-intercept
a0
=
6, then the x-intercept
or zero of the function must be at the point (2,
0).
|
|
Therefore, -
x3
+ 3x2
-
5x
+
6
= - (x
-
2)(x2
-
x
+
3).
|
|
|
|
Equations
with rational expressions |
|
Rational
equations - Linear equations
|
|
|
|
Solve the following
rational equations.
|
|
|
|
|
|
Rational
equations - Quadratic equations
|
|
|
|
Solve the following
rational equations.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
