|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Polynomial and/or
polynomial functions and equations
Polynomial and/or
polynomial functions and equations |
|
|
|
Binomial
equations
|
|
An
equation of the form axn
+
b
=
0, a
> 0, b > 0 and
n is a natural number is
called the binomial
|
|
equation.
|
|
|
|
Solving binomial equations
|
| By using
substitution |
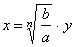 |
the
equation transforms to |
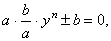 |
or |
y
n
±
1
=
0. |
|
| Recall
that the expression on the left side can be factorized, for example: |
|
y3 +
1
=
(y + 1) · (y2 -
y
+ 1) |
|
y3 -
1
=
(y -
1) · (y2 +
y
+ 1) |
|
y4 +
1
=
(y2
+ 1)2 -
2y2
=
(y2
+ 1 -Ö2
y)
· (y2
+ 1 + Ö2
y) |
|
y4 -
1
=
(y2
-
1) · (y2 +
1)
=
(y -
1) · (y + 1) · (y2 +
1) |
|
y5
+
1
=
(y +
1) · (y4 -
y3 +
y2 -
y
+
1) |
|
y5
-
1
=
(y -
1) · (y4 +
y3 +
y2 +
y
+
1) |
|
y6
-
1
=
( y3 -
1)
· (y3 +
1)
=
(y -
1) · (y + 1) · (y2 +
y
+ 1) · (y2 -
y
+ 1) and so on. |
|
|
|
|
Solve the binomial
equation
8x3
-
27 =
0.
|
|
|
Solution:
Let substitute |
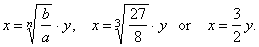 |
|
|
|

|
| To obtain the values of the
original variable plug the solutions into the substitution
x =
(3/2)y |
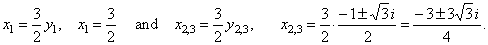 |
|
|
|
|
Solve the binomial
equation
x4
+ 81
=
0.
|
|
|
Solution:
By substituting |
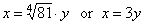 |
obtained
is |
|
|
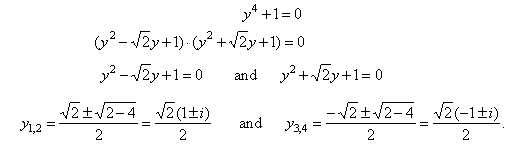
|
|
To obtain the values of the
original variable plug the solutions into the substitution
x =
3y
|
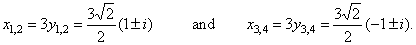
|
|
|
|
Equations
reducible to quadratic form - biquadratic equations
|
|
Solving biquadratic
equations or equations reducible to quadratic
|
|
|
|
Thus, a biquadratic equation ax4
+
bx2
+
c
=
0 we can
write a(x2)2
+
bx2
+
c
=
0
|
|
and
solve as the quadratic equation in the unknown
x2
using the substitution x2
=
y.
|
|
|
|
|
Solve the biquadratic
equation 3x4
-
4x2
+ 1
=
0.
|
|
|
Solution:
By substituting x2
=
y
we get the quadratic equation 3y2
-
4y
+ 1
=
0
|
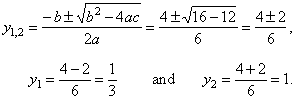
|
|
To obtain the values of the
original variable plug the solutions into the substitution
x2
=
y
|
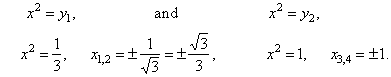
|
|
|
|
|
Solve the equation
x6
-
7x3 -
8 =
0 that is
reducible to quadratic form.
|
|
|
Solution:
By substituting x3
=
y we get the quadratic equation
y2
-
7y -
8 =
0
|
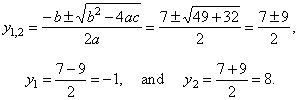
|
|
To obtain the values of the
original variable plug the solutions into the substitution
x3 =
y
|
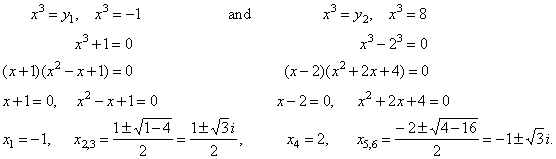
|
|
|
|
Radical
or
irrational
equations
|
| Any
equation where the variable is inside a radical is called an
irrational equation. |
|
Solving irrational
or radical
equations
|
|
|
|
|
Solve the
irrational equation |
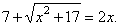 |
|
| Solution:
First isolate the radical and then square both sides
of the equation, |
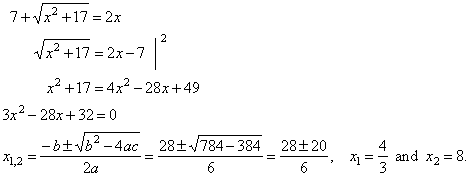 |
| Checking
for the solutions: |
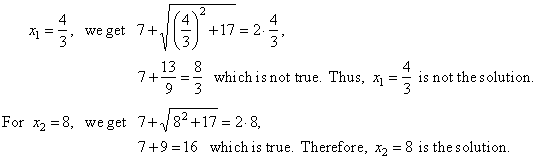 |
|
|
|
|
Solve the
irrational equation |
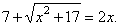 |
|
|
|
| Checking
for the solutions: |
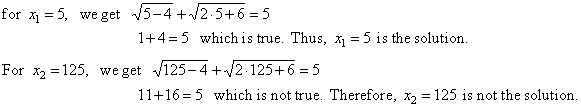 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |