|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Polynomial and/or
polynomial functions and equations
Polynomial and/or
polynomial functions and equations |
|
|
|
Factoring polynomials and
solving
polynomial equations by factoring
|
|
A
polynomial and/or polynomial
function with
real coefficients can be expressed as a product of its leading
coefficient an
and
n
linear factors of the form x
-
xi,
where xi
denotes its real roots and/or complex
roots,
|
|
f (x)
= anxn
+ an-1xn-1
+ . .
. +
a1x
+ a0
= an(x
- x1)(x
- x2)
.
. . (x
- xn).
|
|
Thus, a quadratic or a second
degree polynomial
|
|
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2],
|
|
and
similarly a cubic or a third
degree polynomial
|
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)(x
- x2)(x
- x3)
=
|
|
=
a3[x3
-
(x1 +
x2
+
x3)x2
+
(x1x2 +
x1x3
+
x2x3)x
- x1x2x3]
|
|
and
so on.
|
|
|
|
|
Factorize
(2/3)x2
- (2/3)x
- 4
using
the above theorem.
|
|
|
Solution: (2/3)x2
- (2/3)x
- 4
=
(2/3)(x2
- x
- 6)
=
(2/3)[x2
- (3
+ (-
2))x
+ 3(-
2)] =
|
|
= (2/3)(x2
- 3x
+ 2x
- 6)
=
(2/3)[x(x
- 3)
+ 2(x
- 3)]
=
(2/3)(x
- 3)(x
+ 2).
|
|
|
|
|
Given
are leading
coefficient a2
=
-1and
the pair
of conjugate complex
roots,
x1 =
1 +
i
and
|
|
|
x2
=
1 - i,
of
a second
degree polynomial, find
the polynomial using
the above theorem.
|
|
Solution: By
plugging the given values into a2x2
+ a1x
+ a0 = a2(x
- x1)
(x
- x2)
|
|
a2x2
+ a1x
+ a0 = -1[x
-
(1
+ i)]
· [x
-
(1 - i)]
= -[(x
- 1)
- i]
· [(x - 1)
+ i]
|
|
= -[(x - 1)2
- i2]
=
-(x2
- 2x
+ 1 +
1)
=
- x2
+ 2x
- 2
|
|
|
|
|
Check
the roots of the quadratic found in the previous problem using
the quadratic formula.
|
|
|
|
|
|
|
|
The
real root of the polynomial -
x3
-
x2
+ 4x
- 6
is
x1 =
- 3,
factorize the polynomial.
|
|
|
Solution: We
divide given polynomial by one of its known
factors, since
|
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3)
|
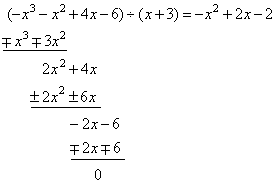
|
|
then
we calculate another two roots of given cubic by solving
obtained quadratic trinomial,
|
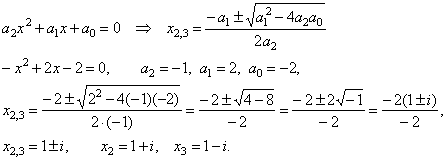
|
|
Finally
we use the theorem to factorize given polynomial (see
the previous example),
|
|
a3(x
- x1)(x
- x2)(x
- x3)
= -1(x
+ 3)[x
-
(1
+ i)][x
-
(1 - i)]
= -(x
+ 3)(x2
- 2x
+ 2).
|
|
Notice that given cubic has one real root and the pair of the conjugate complex roots.
|
|
Odd
degree polynomials must have at least one real root.
|
|
|
|
|
Solve the cubic
equation x3
+ 2x2 -
x -
2 = 0 by factoring.
|
|
|
Solution:
x2(x
+ 2) -
(x + 2) = 0
|
|
(x +
2)·(x2 -
1) = 0
|
|
x +
2 = 0 => x1 =
-2
|
|
x2 -
1 = 0
=>
x +
1 = 0 =>
x2 = -1
|
|
x -
1 = 0 =>
x3 = 1
|
|
Therefore, the roots are,
x1
= -2,
x2 = -1
and x3
= 1.
|
|
|
|
Polynomial functions
|
|
Transformations of the polynomial function
applied to the quadratic and cubic functions
|
|
|
|
Quadratic function
and equation
|
|
y
= f (x)
=
a2x2
+ a1x
+ a0 or
y
-
y0
= a2(x
-
x0)2,
|
| where |
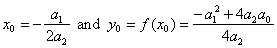 |
coordinates
of translations of the quadratic function. |
|
|
By
setting x0
=
y0
= 0,
we get y
=
a2x2,
the source quadratic function.
The turning point V(x0,
y0).
|
| The
real zeros of the
quadratic function |
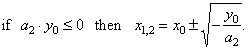 |
|
|
|
|
|
Find zeros and vertex of
the quadratic function y
=
-
x2
+ 2x
+
3
and sketch its graph.
|
|
|
Solution: A quadratic function can
be rewritten into translatable form y
-
y0
= a2(x
-
x0)2
by completing
|
|
the square,
|
|
y
=
-
x2
+ 2x
+ 3 |
Since a2
· y0
<
0 given
quadratic function must have two different real zeros. |
|
y
=
-
(x2
-
2x)
+ 3 |
To find zeros of a function, we set
y
equal to zero and solve for x.
Thus, |
|
y
=
-
[(x
-
1)2
-
1]
+ 3 |
-
4
=
-
(x
-
1)2 |
| y -
4
=
-
(x
-
1)2 |
(x
-
1)2
=
4 |
| y
-
y0
= a2(x
-
x0)2 |
x
-
1
=
+
sqrt(4) |
| V(x0,
y0)
=>
V(1,
4) |
x1,2
=
1
+
2, =>
x1
= -
1
and x2
= 3. |
|
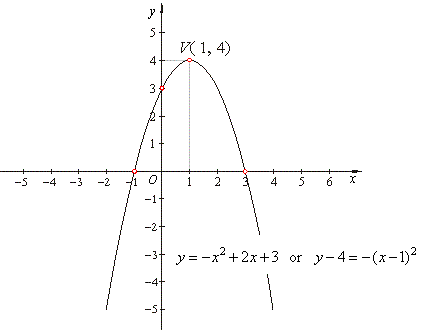
|
|
|
|
Quadratic
inequalities
|
|
|
|
|
Solve the inequality
-
x2
+ 2x
+
3 <
0.
|
|
|
Solution:
Solve the quadratic
equation ax2
+ bx
+
c
= 0
to get the boundary points.
|
|
The zeroes
or roots of equivalent function (see the graph
below) are the endpoints of the intervals and are included in the solution.
|
|
The turning point V(x0,
y0), |
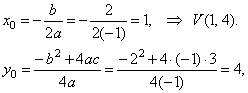 |
|
The roots, -
x2
+ 2x
+
3 =
0 |
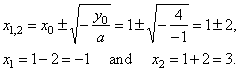 |
|
|
|
| Solution: |
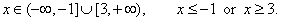 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |