|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
Polynomial and/or
polynomial functions and equations |
| Addition and subtraction of
polynomials |
|
|
|
|
Add or subtract given polynomials.
|
|
|
Solution:
a) ( -
5x3 +
2x2
- x +
4) + ( -
4x2 +
3x - 7)
= - 5x3 +
(
2 -
4) · x2 +
(
-1
+
3) · x +
4 - 7
|
|
= - 5x3 - 2x2 +
2x - 3.
|
|
b) (
x4 -
3x3
+
5x - 1)
-
( - 2x4 +
x3
- 3x2 +
4)
= x4 -
3x3
+
5x - 1
+ 2x4 -
x3
+
3x2 -
4
|
|
= (
1 +
2) · x4
+ (
-3
- 1)
· x3
+
3x2
+
5x - 5
= 3x4 -
4x3
+
3x2
+
5x - 5.
|
|
|
|
Multiplication of polynomials
|
|
|
|
|
Multiply given polynomials.
|
|
|
Solution:
( -
2x3 +
5x2
- x +
1) ·
(
3x - 2)
=
|
|
= 3x · (
- 2x3)
+ 3x · 5x2
+ 3x ·
(-x) + 3x · 1
+ (- 2) · ( -
2x3)
+ (- 2) · 5x2
+ (- 2) · ( -x)
+ (-
2) · 1
|
|
= - 6x4
+ 15x3
- 3x2
+ 3x +
4x3 -
10x2
+ 2x -
2 = -
6x4
+ 19x3
-
13x2
+ 5x -
2.
|
|
|
|
Division of polynomials
|
|
|
|
|
Divide given polynomials.
|
|
|
|
|
Note,
since each second line should be subtracted, the sign of each term is reversed.
|
|
|
|
|
Divide the polynomials (
3x4 +
x2 +
5) ¸
( x2 -
x -
1).
|
|
|
|
|
|
 |
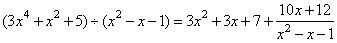| like |
17 ¸
5 = 3 +
2/5 |
| |
-15 |
| |
2 |
|
|
|
|
|
Quadratic equation
|
|
Solving quadratic equations by completing the
square, the quadratic formula
|
|
|
|
|
Solve the quadratic equation ax2
+ bx + c = 0 by
completing the square, derive the quadratic
|
|
|
formula.
|
|
|
|
the
roots can also be written,
|
|
|
|
|
Quadratic equation
word problems
|
|
|
|
|
A train made up for delay of 12 minutes after 60 km of way by running 10 km/h faster then regular
|
|
|
speed.
What is the regular speed of the train?
|
|
|
|
|
|
|
In a theater each row has the same number of seats. Number of rows equals number of seats.
|
|
|
By doubling number
of rows and decreasing number of seats 10 per row, total number of seats in the theater increases by 300. How
many rows are in the theater?
|
|
Solution:
Taking x
as the number of rows (or
seats per row),
then
|
|
|
|
|
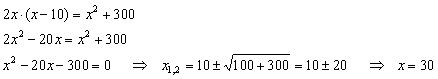
Solving quadratic equations by factoring, Vieta’s formula
|
|
A
quadratic trinomial ax2
+ bx
+ c
can be factorized as
|
|
ax2
+ bx
+ c
= a·[x2
+ (b/a)·x
+ c/a]
= a·(x
-
x1)(x
-
x2)
where, x1
+ x2
= b/a and
x1·
x2
= c/a.
|
|
|
|
|
Find the roots of each
quadratic equation by factoring.
|
|
| Solution: |
a)
x2
- 3x
-10
= 0
|
| since |
x2
- 3x
-10
= x2
+ (-5
+
2)·x
+ (-5)·(+2)
= x2
- 5x
+
2x
-10
|
|
= x (x
- 5)
+ 2 (x
- 5)
= (x
- 5)
(x
+ 2),
|
| then |
x
- 5
= 0
=>
x1 =
5,
and x
+ 2
= 0
=>
x2 =
-2. |
|
|
|
|
b) 2x2
- 7x
+ 3
= 0 |
| since |
2x2
- 7x
+ 3
= 2 [x2
- (7/2)x
+ 3/2]
= 2[x2
- (1/2)x
- 3x
+ 3/2] |
|
= 2[x(x
- 1/2)
- 3(x - 1/2)]
= 2(x - 1/2)(x
- 3)
= (2x
- 1)(x - 3), |
| then |
2x
- 1
= 0
=>
x1 =
1/2,
and x - 3
= 0
=>
x2 =
3. |
|
|
|
|
c) 3x2
- x
- 2
= 0 |
| since |
3x2
- x
- 2
= 3[x2
- (1/3)x
- 2/3]
= 3[x2 +
(2/3)x
- x
- 2/3] |
|
= 3[x(x
+ 2/3)
-
(x + 2/3)]
= 3·(x
+ 2/3)(x
- 1)
= (3x + 2)(x
- 1), |
| then |
3x + 2
= 0
=>
x1 =
-2/3,
or x
- 1
= 0
=>
x2 =
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
