|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
|
|
Rational
Inequalities
|
|
|
|
|
| Solve the rational
inequality
|
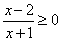 |
and
draw the graph of the rational function. |
|
|
|
Solution:
The solution set of the given rational inequality includes all numbers
x
which make the inequality greater then or equal to 0, or which make the sign of the rational expression
to be positive or 0.
|
|
A rational expression is positive if both the numerator and the denominator are positive
or if both are negative, and the rational expression equals 0 when
its numerator is equal to 0 that is
|
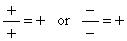
|
|
therefore, we have to solve two simultaneous
inequalities:
|
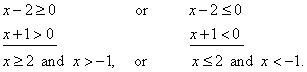
|
|
The solutions represented on the
number line are shown below.
|

|
|
Thus, the solution set of the given
inequality written in the interval notation is (-
oo, -1)
U
[2, oo
).
|
|
The graph of the given rational function is translated equilateral (or rectangular)
hyperbola.
|
| A
rational function of the
form
|
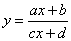 |
can be rewritten into
|
|
|
|
| |
where |
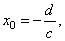 |
the vertical asymptote,
|
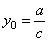 |
the horizontal
asymptote |
|
|
| |
and the
parameter
|
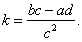 |
|
|
|
Therefore, values of the vertical and
the horizontal asymptote correspond to the coordinates of the horizontal and the vertical translation
of the source equilateral hyperbola y
= k/x, respectively.
|
| Thus, given rational function |
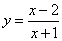 |
where, a
= 1, b
=
-2
and c
=
1,
d
=
1 |
|
| |
has
the vertical asymptote |
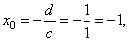 |
|
|
| |
the
horizontal asymptote |
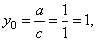 |
|
|
| |
and
the parameter |
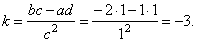 |
|
|
| Therefore,
its source function is the equilateral or rectangular
hyperbola |
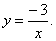 |
|
|
|
The graph of given rational function is shown
below, (see the above example of the rational inequality).
|
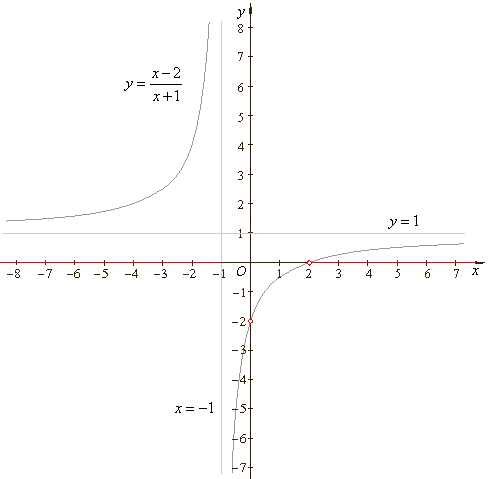
|
|
|
|
|
Solve the rational
inequality
|
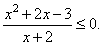 |
|
|
|
Solution:
The solution set of the given rational inequality includes all numbers
x
which make the inequality less then or equal to 0, or which make the sign of the rational expression
to be negative or 0.
|
|
A rational expression is negative if the numerator and the denominator
have different signs, and the rational expression equals 0 when
its numerator is equal to 0 that is,
|
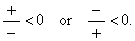
|
|
therefore, we have to solve two simultaneous
inequalities.
|
|
We graph the numerator and the
denominator in the same coordinate system to find all points of
the x-axis
that satisfy given inequality.
|
|
The zero points of the numerator and
the denominator divide the x-axis
into four intervals at which given rational expression changes
sign.
|
| x2
+ 2x -
3 = 0, a = 1, b = 2 and
c = -3
|
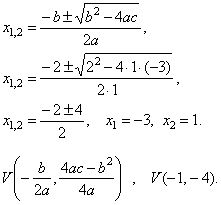
|
|
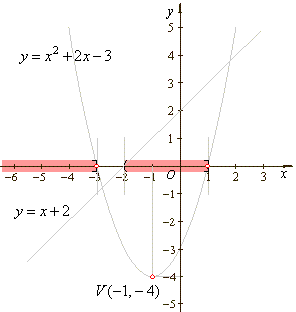 |
|
|
The solutions of the two pairs of the simultaneous
inequalities are intersections of sets of their partial solutions,
|
|
|
|
as is shown below.
|
|
|
|
Therefore, the solution set is (
-
oo,
-3]
U
( -2,
1].
|
|
|
| Absolute value
inequalities |
| Solving
linear inequalities with absolute value |
| Graphical
interpretation of the
definition of the
absolute value of a function y =
f(x) will help us solve
linear inequality with absolute value. |
|
|
| 96. |
Solve the absolute value
inequality | x
-
2
| < 3.
|
|
| Solution:
Graphical
interpretation of the given inequality will help us find
values of x
for which left side of the inequality is less then or equal to
3. |
| For
values of x
for which y
is nonnegative, the graph of | y
| is the
same as that of y =
x -
2.
|
| For values of
x
for which y
is
negative, the graph of | y
| is a reflection of
the graph of y
across the x
axis. |
| Since
the graph of y =
x -
2 has y
negative on
the interval (-
oo, 2) it is this part of the graph
that has to be reflected on the x
axis. |
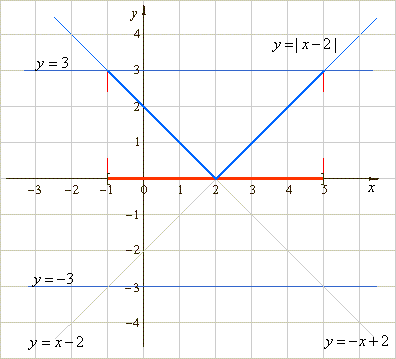 |
| The
graph shows that
values of x from
the closed interval [-1,
5] satisfy the given inequality. |
| The
same result can be obtained algebraically by solving the
compound inequality. |
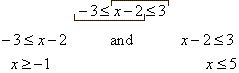 |
 |
| x
Î [-1,
5] |
|
|
|
|
| 97. |
Solve the absolute value
inequality | x
-
2
| > 3.
|
|
| Solution:
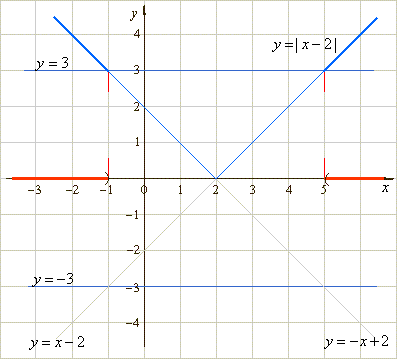
Again, graphical
interpretation of the given inequality will help us find
values of x
for which left side of the inequality is greater than 3. |
| The
graph shows that
values of x from
the open intervals, (- oo, -1)
or (5,
oo)
satisfy the given inequality. |
 |
| The
same result can be obtained algebraically by solving the two
inequalities |
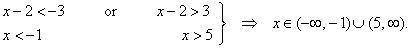 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |