|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Linear
inequalities
Linear
inequalities
|
| Solving linear
inequalities |
|
|
|
|
|
|
Solve given linear inequality.
|
|
| Solution: |
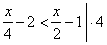 |
|
x -
8
< 2x
-
4 |
|
- x
<
4
|
·
(-1) |
|
x
>
-4 |
|
 |
| The
solution of the inequality is every real number greater
than -4. |
|
|
|
|
| 87. |
Solve inequality
3(x -
2) >
-2(1-
x).
|
|
| Solution:
3x -
6
>
-2
+
2x |
|
x > 4 |
|
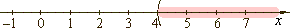 |
|
interval
notation
(4, oo) |
|
|
| The
open interval (4, oo)
contains all real numbers between given endpoints, where round
parentheses indicate exclusion of endpoints. |
|
|
| 88. |
Solve given linear inequality.
|
|
|
Solution:
|
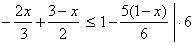 |
|
-4x
+
9 -
3x
<
6 - 5
+
5x |
|
-12x
<
-8 |
|
x
>
2/3 |
|
|
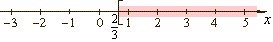 |
| interval
notation |
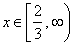 |
|
|
| The
half-closed (or half-open) interval
contains all real numbers between given endpoints, where the
square bracket indicates inclusion of the endpoint 2/3 and round
parenthesis indicates exclusion of infinity. |
|
|
| 89. |
Solve inequality
(x
- 3)
· (x
+ 2)
> 0
|
|
| Solution:
The factor
x
- 3
has the zero at x
= 3, is negative for x
< 3
and is positive for x
> 3,
and |
| the factor
x
+ 2
has the zero at x
= -2,
is negative for x
< - 2
and is positive for x
> -2, |
| as
is shown in the table |
| x |
-
oo |
increases |
-2 |
increases |
3 |
increases |
+
oo |
| x
+ 2 |
|
- |
0 |
+ |
+ |
+ |
|
| x
- 3 |
|
- |
- |
- |
0 |
+ |
|
| (x
- 3)(x
+ 2) |
|
+ |
0 |
- |
0 |
+ |
|
|
|
| Thus,
the given inequality is satisfied for -
oo
< x
< - 2
or 3
< x
< + oo |
|
in the interval notation (-
oo
, -2]
U [3,
+ oo
) |
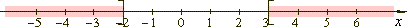 |
|
|
|
Solving
compound (double) inequalities
|
|
|
| 90. |
Solve inequality
-4
< 2(x
- 3)
< 5
|
|
| Solution:
We want the x alone as middle term and only constants in the two outer terms. Remember,
while simplifying given compound inequality, the operations that we apply to a middle term we
should also do to the both left and right side of the inequality. |
|
|
|
|
|
|
|
|
|
|
Solve given linear inequality.
|
|
|
|
|
|
|
|
|
Systems
of linear inequalities
|
|
The solution of the system of
simultaneous inequalities is the intersection of sets
of the individual solutions.
|
|
|
| 92. |
Solve and graph the
solution of the given system of simultaneous inequalities.
|
|
|
|
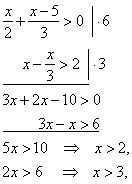 |
|
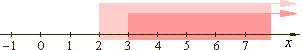 |
| the solution of the system
is the open interval (3, + oo
). |
|
|
|
|
Solving and graphing systems of
linear inequalities in two variables
|
|
The set of points whose coordinates (x,
y)
satisfy the inequality ax+
by + c > 0 is a
half-plane of a Cartesian plane.
|
|
|
| 93. |
Solve and graph the
solution of the given system of linear inequalities in two
variables.
|
|
| Solution:
|
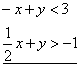 |
| Plug the
coordinates of the origin |
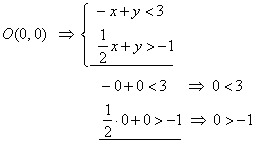 |
|
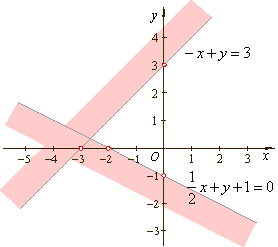 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |