|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Linear
equations
in one variable
Linear
equations
in one variable
|
|
|
|
Absolute value
equations
|
|
Solving absolute value
equations
|
|
|
|
|
| Solution:
1
-
2x =
17
or
1 -
2
x = -17 |
|
2
x = - 16
2x =
18 |
|
x = -
8
x = 9 |
| The
solutions to the given equation are
x = - 8
and
x = 9. |
|
|
|
|
| Solution:
-3
-
x = 5
or
-3
-
x = -5 |
|
x = -
8
x = 2 |
| The
solutions to the given equation are
x = - 8
and
x = 2. |
|
|
|
|
| Solution:
x + 1 = 2x
-
3
or
x + 1 = -(2
x -
3) |
|
x - 2x
= - 4
x +
2x = 3 -
1 |
|
x = 4
3x = 2
=> x = 2/3 |
| Check
solutions: |
| x = 4
=>
|
x + 1 | =
2x -
3,
x = 2/3
=>
|
x + 1 | =
2x -
3 |
|
|
4
+ 1 | =
2 · 4 -
3
|
2/3 + 1 | =
2 · 2/3 -
3
|
|
5 = 5
5/3
is not
-5/3 |
| The
check shows that x =
2/3 is not a solution,
because the right side of the equation becomes negative. There is a single solution to this equation: x = 4. |
|
|
| 82. |
|
x + 2 | =
| 2x -
5 |
|
|
|
Solution:
As both
sides of the equation contain absolute values the
only way the two sides are equal is,
|
| the
two quantities
inside the absolute value bars are equal or equal but with
opposite signs.
|
|
x + 2 = 2x
-
5
or
x + 2 = -(2
x -
5) |
|
x -
2x
= -
5 -
2
x + 2 = -2
x +
5 |
|
-x =
-7
3x = 3 |
|
x = 7
x = 1 |
| Check
solutions: |
| x =
7 =>
|
x + 2 | =
| 2x -
5 |, x = 1
=>
|
x + 2 | =
| 2x -
5 | |
|
|
7 + 2 | =
| 2 · 7 -
5
|
|
1 + 2 | = | 2 ·
1 -
5 |
|
|
9 = 9
3 = | -3 | |
| Therefore,
the
solutions to the given equation are x =
7 and x =
1. |
|
|
Linear equation with
absolute value, graphic solution
|
|
|
|
|
| Solution: |
|
| -3
-
x = 2 or
-3
-
x = -2 |
|
x = -
5
x = -1 |
|
| The
solutions to the given equation are |
|
x = - 5
and x = -1. |
|
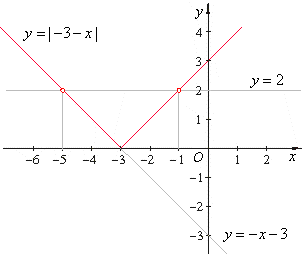 |
|
|
|
|
|
| Solution:
x + 1 = 2x
-
3
or
x + 1 = -(2
x -
3) |
|
x - 2x
= - 4
x +
2x = 3 -
1 |
|
x = 4
3x = 2
=> x = 2/3 |
| Check
solutions: |
| x = 4
=>
|
x + 1 | =
2x -
3,
x = 2/3
=>
|
x + 1 | =
2x -
3 |
|
|
4
+ 1 | =
2 · 4 -
3
|
2/3 + 1 | =
2 · 2/3 -
3
|
|
5 = 5
5/3
is not
-5/3 |
| The
check shows that x =
2/3 is not a solution,
because the right side of the equation becomes negative. There is a single solution to this equation: x = 4. |
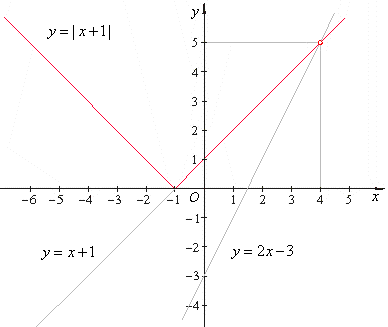 |
|
|
| 85. |
|
x + 2 | =
| 2x -
5 |.
|
|
|
Solution:
As both
sides of the equation contain absolute values the
only way the two sides are equal is, the two quantities
inside the absolute value bars are equal or equal but with
opposite signs.
|
|
x + 2 = 2x
-
5
or
x + 2 = -(2
x -
5) |
|
x -
2x
= -
5 -
2
x + 2 = -2
x +
5 |
|
-x =
-7
3x = 3 |
|
x = 7
x = 1 |
| Check
solutions: |
| x =
7 =>
|
x + 2 | =
| 2x -
5 |, x = 1
=>
|
x + 2 | =
| 2x -
5 | |
|
|
7 + 2 | =
| 2 · 7 -
5
|
|
1 + 2 | = | 2 ·
1 -
5 |
|
|
9 = 9
3 = | -3 | |
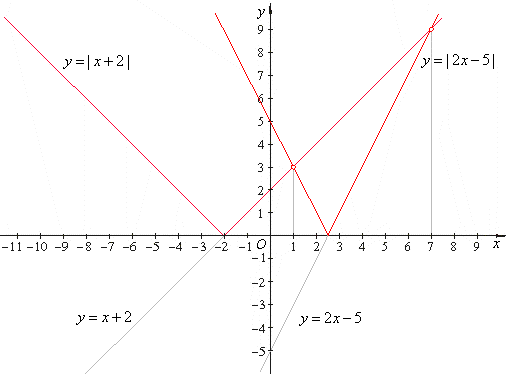 |
| Therefore,
the
solutions to the given equation are x =
1 and x =
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |