|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Linear
equations
in one variable
Linear
equations
in one variable
|
|
|
Miscellaneous word
problems
|
|
|
| 70. |
If fresh grapes contain 90% water and dried 12%, how much dry grapes we get from 22 kg of fresh
|
|
| grapes?
|
|
Solution:
Fresh grapes contain 90% water and 10% dry substance.
|
|
Dry grapes contain 12% water and 88% dry substance.
|
| 22 kg of fresh grapes = x kg
of dry grapes, so |
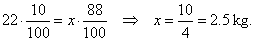 |
|
|
| 71. |
An amount decreased 20% and then increased 50%, what is the total increase in relation to initial
|
|
| value.
|
|
Solution: An initial amount
x decreased by 20%, |
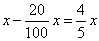 |
|
|
The obtained amount increased by 50%, |
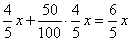 |
|
|
The difference in relation to the initial value x,
|
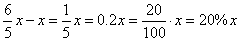 |
|
|
shows increase by 20%.
|
|
| 72. |
From a total deducted is 5% for expenses and the remainder is equally divided to three persons.
|
|
|
What was the total
if each person gets $190?
|
|
Solution: If
x
denotes the total then |
 |
|
|
|
|
|
| 73. |
Into 10 liters of the liquid
A poured is 4 liters of the liquid
B
and 6 liters of the liquid
C.
|
|
|
From obtained mixture D
poured is out 3 liters, how many liters of the liquid C
remains in the mixture
D?
|
|
Solution:
A
+ B
+ C
= D => 10 l + 4 l + 6 l = 20 l
|
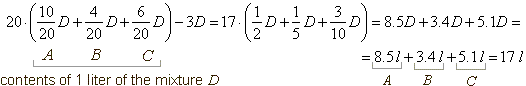
|
|
|
| Variable expressions
(expressions involving variables) and formula problems |
| Solving
a formula for a specified variable, transposition of a
formula (changing the subject of
a formula) |
|
| 74. |
Into a cistern are poured 37.4 tonnes of petrol and remains 6.5% of the cistern not filled.
|
|
| How many tonnes of the petrol will fit in the cistern to be full.
|
|
Solution:
Applying the
proportion B :
A
=
100% :
p,
|
| where
A = 37.4 tonnes or 93.5%
denotes the amount (that
correspond to percentage), B
is base (correspond |
|
to the whole or 100%) and p
is percent, it follows that |
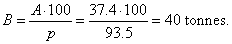 |
|
|
| 75. |
Fresh figs contain 90%
of water and dry figs contain 12%. How many kilos of dry figs are obtained
|
|
|
by drying 264 kg of fresh
figs?
|
|
Solution:
Using the
proportion B
:
(B
± A)
= 100 :
(100
± p),
|
|
As fresh figs contain 10% of the dry substance and dry figs contain 88% of the dry
substance it follows that
|
| 264 kg of fresh figs contains 26.4 kg of the dry substance.
|
| Therefore, 26.4 kg is 88% of quantity of dry figs or it is
weight of the dry figs decreased by 12% of water, |
| so
B -
A = 26.4 kg,
and by using the above formula |
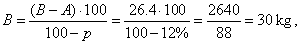 |
| obtained
is the
weight of the dry figs. |
|
|
| 76. |
Sum of all three-digits numbers divisible by 3 is?
|
|
|
Solution: The
three-digits numbers divisible by 3
are;
|
|
102, 105, 108, .
. . , 996, 999
|
| and
they represent the arithmetic
progression |
|
a1,
a2,
a3, .
. . , an
- 1,
an,
where a1
= 102, an
= 999 and d
= 3, |
| since
an
= a1 + (n - 1)
· d then 999
= 102 + (n - 1)
· 3
|
|
3
· (n - 1)
= 897 | ¸3
|
| n
- 1
= 299
=> n
=
300 |
| Using the
sum formula, |
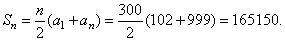 |
|
|
|
| 77. |
How many minutes pass while watch hands coincide again?
|
|
|
Solution: Suppose watch hands last coincide at noon. They will
coincide again 5 to 6 minutes after 13 hours.
|
| To reach 13 hours, the minute hand traveled full circle 360° or 60 minutes,
and the hour hand traveled 30°.
|
|
Therefore, the minute hand travels at speed of |
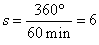 |
degrees per minute, |
|
| while the hour hand travels at speed of |
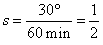 |
degree per minute. |
|
|
Hands will coincide again the minute hand passes additional distance of
30° +
x° while, at the same time, the hour hand passes the distance of
x°, i.e.,
|
|
|
| Thus, watch hands will coincide again after
60 min + 5 min + 5/11 min = 65 and 5/11 min. |
|
|
|
|
If v = g t + v0
and |
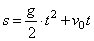 |
then t is
equal?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |