|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Linear
equations
in one variable
Linear
equations
in one variable
|
|
|
Time and travel problems - Distance, rate (or speed) and time relations
|
|
|
| 60. |
A
rider has to catch a pedestrian up who is already 7 hours on his route. How
long it will take if
|
|
|
the rider travels at the rate of 12 kilometers per hour
and the pedestrian travels at 5 kilometers per hour?
|
|
In time and travel problems we use the
following distance, rate and time relations:
|
| |
distance
= rate ´
time, |
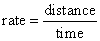 |
and
|
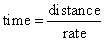 |
. |
|
|
|
Solution:
The
same distance rider travels x
hours, the pedestrian travels (x
+ 7) hours,
|
|
since, distance
= rate ´
time, then
12 · x =
5 · (x + 7)
|
|
12x = 5x + 35
|
|
7x =
35
|
|
x = 5 hours.
|
|
| 61 |
To
travel the distance between two stations a passenger train, traveling at rate
of 12 meters per
|
|
| second, takes 16 minutes and 40 seconds less than a freight
train moving at speed of 8 meters per second.
|
| What is the distance?
|
|
Solution:
We
equate the times denoting the distance by x,
|
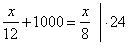 |
|
where, 16 minutes and 40
seconds = 1000
seconds |
|
|
2x + 2400 = 3x
|
|
x = 24000 meters
= 24 kilometers
|
|
|
| 62. |
A
walker walking at the rate of 1 kilometer in 12 minutes travels a distance from A to
B and spend
|
|
|
the same time as a cyclist who travels 10 kilometers longer
distance riding at speed of 1 km in four and the
|
|
half minutes. What is the
distance from A to B?
|
|
Solution:
Walker
took a way of x
kilometers at the rate of 1/12 kilometers per minute through the time
|
|
of x/
(1/12) minutes.
|
|
The cyclist travels (x +
10)
kilometers at the rate of 1/(4 and 1/2) kilometers per minute through the time
|
|
of (x +
10) / [1/(4
and 1/2)] minutes.
|
|
They traveled the same period of time, thus
|
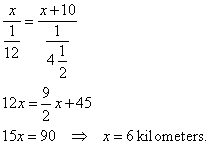
|
|
|
|
Geometry word problems
|
|
The
general procedure to solve a geometry word problem is:
|
| 1.
Draw a sketch of the geometric figure. |
| 2.
Label its elements using information given in the problem. |
| 3.
Choose the correct formula for the
given problem (ex: perimeter, area, volume etc.). |
| 4.
Substitute the data from the problem into the formula. |
| 5.
Solve it for the unknown. |
|
| 63. |
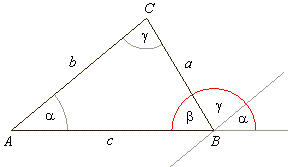
The
angle g
of a triangle is twice as large as the
angle a,
and the angle b is
three-fourth of the
|
|
| angle g.
What are the angles measures?.
|
|
Solution: |
|
given, g
= 2a
and b
= 3/4g
= 3/4 ·
2a =
3/2a |
|
since,
a
+
b +
g
= 180° |
|
then
a
+ 3/2a
+ 2a
= 180° |
|
9/2a
= 180°
=> a
= 40° |
|
b
= 3/2a
= 3/2 ·
40 =
60° |
|
g
= 2a
= 2 · 40°
= 80° |
|
 |
|
|
| 64. |
The
exterior angles that lie on the hypotenuse of a right triangle are in the
ratio of 11 : 16, find the
|
|
|
angles.
|
|
Solution: |
|
r2
= (r
- 8)2
+ (c/2)2
|
|
r2 = (r - 8)2
+ 122
|
| r2
= r2
- 16r
+ 64
+ 144
|
| 16r
= 208 |
|
r = 13 cm |
|
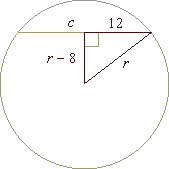 |
|
|
|
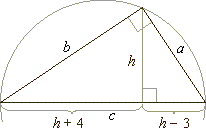
| 65. |
The
height of a right triangle is 3 units longer than the orthogonal projection of
the shorter leg on the
|
|
|
hypotenuse and 4 units smaller than the projection of
the longer leg. Find lengths of the projections
|
|
(segments).
|
|
Solution:
Using similarity of the two right triangles, |
|
(h
+
4)
: h = h
: (h
- 3)
|
|
h2 =
(h
+ 4) · (h - 3)
|
| h2 =
h2
+ h
- 12
=> h
= 12
|
| p
= h - 3
= 12 - 3
= 9, |
|
q
= h
+ 4
= 12
+ 4
= 16,
c
= p +
q
= 25 |
|
 |
|
|
| 66. |
Sides
of a rectangle are in the ratio of 3
: 5. If the length
is decreased by 4 cm and the width is
|
|
| increased by 1 cm, its area will be
decreased by 39 cm2. Find dimensions of the rectangle. |
|
Solution:
a
: b = 3
: 5 =>
a = (3/5) · b |
|
A = a · b = (3/5)b
· b
|
| [(3/5)b
+ 1] · (b - 4)
= (3/5)b
· b
- 39
|
|
(3/5)b2
- 7/5b
- 4
= (3/5)b2
- 39 |
|
7/5b =
35
a = (3/5) ·
b = (3/5) · 35 |
|
b = 25 cm,
a = 15 cm, |
|
 |
|
|
| 67. |
If number of sides of a polygon increases by 3 then the number of its
diagonals increases by 18.
|
|
| Which polygon has this properties? |
|
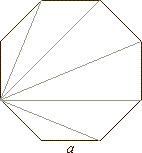
Solution:
Since an
n-sided polygon has
n
vertices, and from each vertex can be drawn (n
- 3)
diagonals, then the total number of diagonals that can be drawn is n
· (n - 3). However,
as each diagonal joins two vertices, this means that each diagonal will be drawn twice, so the expression must be divided by 2.
|
| Thus, number of diagonals of an n-sided
polygon, dn
= n
· (n - 3)
/ 2.
|
|
| By substituting the given condition
|
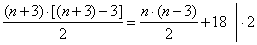
|
| (n
+ 3) · n = n
· (n - 3)
+ 36
|
|
n2
+ 3n = n2
- 3n
+ 36 |
|
6n = 36 =>
n =
6 |
|
 |
|
|
|
| 68. |
Of which regular polygon, the difference between the interior and
exterior angle, is 132°.
|
|
|
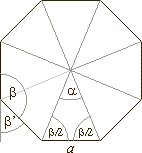
Solution:
In a regular polygon a
= 360°/n
and a
+
b
= 180°,
therefore a
= b', as shows the picture.
|
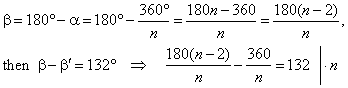
|
|
180n
- 360
- 360 =
132n
|
|
48n
= 720 => n
= 15
|
|
 |
|
|
|
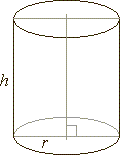
| 69. |
The ratio of the lateral area of a cylinder to its surface area is 5 :
8. Find the radius of the base if it
|
|
|
is 8 cm shorter than the height of the
cylinder.
|
|
Solution: The
lateral area of the cylinder Slat =
2rp
· h = 2rp(r
+ 8),
|
|
and the surface area S =
2B + Slat =
2r2p
+ 2rp(r
+ 8).
|
|
|
given
Slat
: S = 5 :
8
|
|
2rp(r
+ 8)
:
[2r2p
+ 2rp(r
+ 8)] =
5 :
8
|
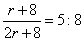
|
|
8r
+ 64 = 10r
+ 40
|
|
2r
= 24 => r
= 12
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |