|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Linear
equations
in one variable
Linear
equations
in one variable
|
|
|
|
Word
problems that lead to simple linear equations
|
| Number
problems |
|
| The
general procedure to solve a word problem is:
1.
Set the unknown. |
|
2.
Write equation from the text of the problem.
3.
Solve the equation for the unknown. |
|
| 51. |
A number multiplied by 5
and divided by 4 equals twice the number decreased by 15.
|
|
|
Solution:
Let x
denotes the number, then |
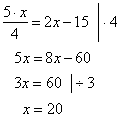 |
|
| 52. |
Split the number 61 into
two parts so that quarter of the first part increased by sixth
of the other
|
|
| part gives 12. What are these parts? |
|
Solution:
Let x
denotes the first part of
the number, then |
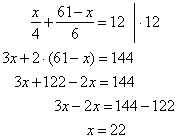 |
|
|
Age problems |
|
|
| 53. |
A father is 48 years old
and his son is 14.
|
|
|
a) In how many years will the father be three times older
then his son? |
|
b) How many years before was the father seven times older
then his son? |
|
Solution:
After x
years a) 48
+ x = 3 ·
(14 + x) |
|
48 + x = 42 + 3x |
|
x -
3x = 42 -
48 |
|
-2x
= -6
| ¸
(-2) |
|
x = 3 years. |
|
|
Before x
years b) 48
-
x = 7 · (14 -
x) |
|
48 -
x = 98 -
7x |
|
7x -
x = 98 -
48
|
|
6x = 50
|
|
x = 25/3 = 8 years and 4
months.
|
|
|
|
Mixture problems
|
|
|
| 54. |
If we mix Qa
liters of vine, of Ca
dollars per liter, with Qb
liters of vine, of Cb
dollars per liter, how
|
|
|
much will cost one liter of the
mixture
|
|
Where; Qa= quantity
of a,
Ca= cost of a,
|
|
Qb=
quantity of b,
Cb= cost of b.
|
|
Solution:
If CM
denotes the cost of one liter of the mixture, then |
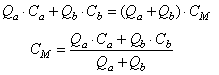
|
|
|
| 55. |
How
much liters of vine of $8 per liter should mix with 15 liters of vine of $14
per liter to get
|
|
| mixture that will cost $10 per liter.
|
|
Solution:
Using the above equation,
Qa · Ca +
Qb · Cb =
(Qa +
Qb)
· CM
|
|
x · 8 + 15 · 14 = (x + 15) · 10
|
|
8x + 210 = 10x + 150
|
|
2x = 60
|
|
x = 30 liters
|
|
| 56. |
By
mixing alcohol of 50% strength with alcohol of 80% we get 12 hectoliters of
alcohol of 70%
|
|
| strength. How much of each kind of alcohol was combined?
|
|
Solution:
If x
denotes amount of alcohol of 50% strength, then
|
|
x · 50 + (12 -
x) · 80 = 12 · 70
|
|
50x + 960 -
80x = 840
|
|
30x = 120
|
|
x = 4 hectoliters
|
|
Therefore, combined are 4
hectoliters of alcohol of 50% strength and
8 hectoliters of alcohol of 80% strength.
|
|
|
Work problems
|
|
|
| 57. |
One
of two workers can finish a job for 15 days, and other for 10 days, how long
will it take to
|
|
|
finish the job working together.
|
|
Solution:
The first worker does 1/15 of the job per day, and the second worker does 1/10 of the job per day.
|
|
If working together they complete the job
in x
days, then
|
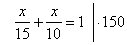
|
|
10x + 15x = 150
|
|
25x = 150
|
|
x = 6 days.
|
|
|
| 58. |
Suppose
a person A can finish a job in 12 days. He worked three days when a person B
joins him
|
|
|
to help. Suppose the person B can finish the same job in 15 days.
How long will they take to finish the job?
|
|
Solution:
If working together they complete the job
in x
days, then
|
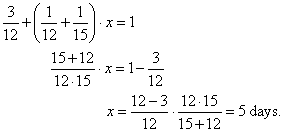
|
|
| 59. |
A
tank can be filled with three pipes:
|
|
|
- first pipe (alone) takes 10 hours (a
= 10) to fill the tank,
|
|
- second pipe takes 12 hours (b
= 12),
|
|
- third pipe takes 15 hours (c
= 15) to fill the tank.
|
|
How long would it take to fill the tank with
water,
|
|
a) if all pipes are opened at the same time,
|
|
b) if second and third pipes fill the tank while at the same time water
leaking from the tank
|
|
through the first pipe?
|
|
Solution: a)
first pipe fills 1/a
part of the tank per hour, second pipe fills 1/b
and third pipe fills 1/c
part of the
|
|
tank per hour. It will take x
hours to fill the thank, thus
|
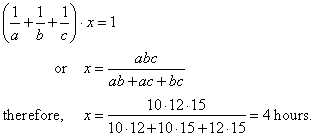
|
|
|
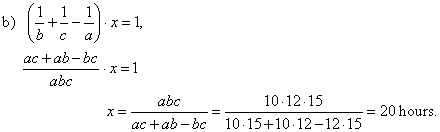
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |