|
|
|
ALGEBRA
- solved problems
|
|
|
|
|
|
|
|
 Algebraic
expressions
Algebraic
expressions
|
|
 Factoring and
expanding algebraic
expressions, rules
for transforming algebraic
expressions
Factoring and
expanding algebraic
expressions, rules
for transforming algebraic
expressions |
| Expanding algebraic
expressions |
|
The
square of a binomial, a perfect square trinomial |
|
(a +
b)2 = a2
+ 2ab
+
b2, |
|
|
(a
- b)2 =
a2
- 2ab
+
b2, |
|
|
The
square of a trinomial |
|
(a - b
+
c)2 = a2
+ b2
+ c2
- 2ab
+ 2ac
- 2bc, |
|
|
The
cube of a binomial |
|
(a + b)3
= a3 + 3a2b
+
3ab2
+ b3, |
|
|
(a - b)3
= a3
- 3a2b
+
3ab2
- b3, |
|
| Factoring algebraic
expressions |
|
Difference of
two
squares |
|
|
x2
- y2
= (x - y)
·
(x
+
y), |
|
|
Sum and difference of cubes |
|
x3 - y3
= (x - y)
·
(x2
+ xy
+ y2), |
|
|
x3 +
y3
= (x + y)
·
(x2 - xy
+ y2). |
|
|
| The
sum and/or difference of any two numbers raised to the same
(positive integer) power |
|
x4
- y4
= (x - y)
·
(x3 + x2y
+ xy2
+ y3)
=
(x2
- y2)
·
(x2 +
y2) |
|
|
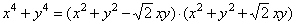 |
|
|
|
|
|
|
|
x2n
- y2n
= (x - y)
·
(x2n-1 + x2n-2y
+
. . . + xy2n-2
+ y2n-1)
= (xn
- yn)
·
(xn +
yn) |
|
|
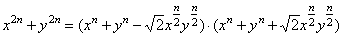 |
|
|
|
|
|
|
| The binomial expansion
algorithm - the binomial theorem |
| The
binomial expansion of any positive integral power of a binomial,
which represents a polynomial with n
+ 1 terms, |
|
|
|
or written in the form of the sum formula
|
|
|
|
|
| is
called the binomial theorem. |
| The
binomial coefficients can also be
obtained by using Pascal's triangle. |
| The
triangular array of integers, with 1 at the
apex, in which each number is the sum of the two
numbers above it in the preceding row, as is
shown in the initial segment in the diagram, is
called Pascal's triangle. |
|
| So,
for example the last row of the triangle
contains the sequence of the coefficients of a
binomial of the 5th power. |
|
|
| n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
| 1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
| 2 |
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
| 3 |
|
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
| 4 |
|
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
| 5 |
|
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
|
| - |
1 |
|
- |
|
- |
|
- |
|
- |
|
- |
|
1 |
|
|
|
| 16. |
Expand the binomial using the binomial theorem.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |