|
|
|
ALGEBRA
- solved problems
|
|
|
|
|
|
|
|
 Algebraic
expressions
Algebraic
expressions
|
|
| Factoring
quadratic trinomials |
|
| A
quadratic trinomial ax2
+ bx
+ c
can be factorized as |
| ax2
+ bx
+ c
= a·[x2
+ (b/a)·x
+ c/a]
= a·(x
-
x1)(x
-
x2), |
where
x1
+ x2
= b/a and
x1·
x2
= c/a |
|
|
| 11. |
Factorize quadratic trinomials.
|
|
|
Solutions:
|
|
a) x2
- 3x
-10
= x2
+ (-5
+
2)·x
+ (-5)·(+2)
= x2
- 5x
+
2x
-10
= |
|
|
|
= x ·
(x
- 5)
+ 2 ·
(x
- 5)
= (x
- 5)
·
(x
+ 2), |
|
|
|
|
|
b) 2x2
- 7x
+ 3
= 2 ·
(x2
- 7/2x
+ 3/2)
= 2(x2
- 1/2x
- 3x
+ 3/2)
= |
|
|
= 2[x·(x
- 1/2)
- 3·
(x - 1/2)]
= 2·
(x - 1/2)·(x
- 3)
= (2x
- 1)·
(x - 3), |
|
|
|
|
|
c) 3x2
- x
- 2
= 3(x2
- 1/3x
- 2/3)
= 3(x2 +
2/3x
- x
- 2/3)
= |
|
|
= 3[x·(x
+ 2/3)
-
(x + 2/3)]
= 3·(x
+ 2/3)·(x
- 1)
= (3x + 2)·(x
- 1). |
|
|
| 12. |
Given
are leading
coefficient a2
=
-1
and
the complex
roots,
x1 =
1 +
i
and
x2
=
1 - i,
of
a
|
|
| second
degree polynomial, find
the polynomial using
the above theorem. |
| Solution:
|
By
plugging the given values into a2x2
+ a1x
+ a0 = a2(x
- x1)
(x
- x2) |
|
a2x2
+ a1x
+ a0 = -1[x
-
(1
+ i)]
· [x
-
(1 - i)]
= -[(x
- 1)
- i]
· [(x - 1)
+ i] |
|
= -[(x - 1)2
- i2]
=
-(x2
- 2x
+ 1 +
1)
=
- x2
+ 2x
- 2. |
|
|
| Factoring
cubic or a third degree polynomial |
| |
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3)
= |
|
|
| |
=
a3[x3
-
(x1 +
x2
+
x3)x2
+
(x1x2 +
x1x3
+
x2x3)x
- x1x2x3]. |
|
|
| 13. |
The
real root of the polynomial -
x3
-
x2
+ 4x
- 6
is
x1 =
- 3,
factorize the polynomial.
|
|
| Solution:
|
We
divide given polynomial by one of its known
factors, |
|
a3x3
+ a2x2
+ a1x
+ a0 = a3(x
- x1)
(x
- x2)
(x
- x3) |
|
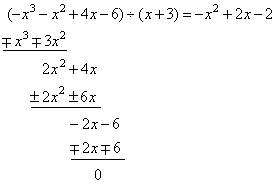 |
|
then
we calculate another two roots of given cubic by solving
obtained quadratic trinomial, |
|
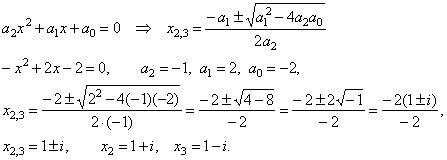 |
|
Finally
we use the theorem to factorize given polynomial (see
the previous example), |
|
a3(x
- x1)(x
- x2)(x
- x3)
= -1(x
+ 3)[x
-
(1
+ i)][x
-
(1 - i)] |
|
= -
(x
+ 3)(x2
- 2x
+ 2). |
|
Notice that given cubic has one real root and the pair of the conjugate complex roots. |
|
Odd
degree polynomials must have at least one real root. |
|
|
|
Sum and difference of cubes |
|
| 14. |
Factorize given sum and difference of cubes.
|
|
|
Solutions:
|
|
a) x3
+ 8
= x3 + 23
= (x + 2)
·
(x2
- 2x
+ 22), |
|
|
|
since (x + 2)·(x2
- 2x
+ 4)
= x3
- 2x2
+ 4x
+ 2x2
- 4x
+ 8
= x3
+ 8, |
|
|
|
|
|
b) 8a3
-125
=
(2a)3 -
53
= (2a - 5)·
[(2a)2
+
(2a)·5 + 52]
= (2a - 5)(4a2
+ 10a
+ 25), |
|
|
since (2a
- 5)(4a2
+ 10a
+ 25)
= 8a3 +
20a2
+ 50a
- 20a2
- 50a
-125
= 8a3 -125. |
|
|
| Using
a variety of methods including combinations of the above to
factorize expressions |
|
| 15. |
Factorize given expressions.
|
|
|
Solutions:
|
|
a) x2
- 2xy
+ y2
+ 2y
- 2x
=
(x
- y)2
- 2(x
- y)
=
(x
- y)(x
- y
- 2), |
|
|
|
|
|
|
b) x2
- y2
+ xz
- yz
=
(x
- y)(x
+ y)
+ z(x
- y)
= (x
- y)(x
+ y
+ z), |
|
|
|
|
|
c) 4x2
- 4xy
+ y2
- z2
= (2x - y)2
- z2
=
(2x
- y
- z)(2x
- y
+ z), |
|
|
|
| d) a3
- 7a
+ 6
= a3 - a
- 6a
+ 6
= a(a2 -1)
- 6(a
-1)
= (a -1)·[a(a
+ 1)
- 6]
= (a -1)(a2
+ a
- 6)
|
|
= (a -1)(a2
+ 3a
- 2a
- 6)
= (a -1)[a(a
+ 3)
- 2(a
+ 3)]
= (a -1)(a
+ 3)(a
- 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |