Interest calculations, Simple interest, Compound interest

ALGEBRA - solved problems

Interest calculations

Simple interest

111.

Somebody deposits $20,000 into a savings account where the rate of interest is 4.8% annually.

How much money in interest will earn after nine months?

An amount of money deposited into a bank for a given period of time brings to the depositor a profit called interest.

The amount of interest (I ) the bank pays you, depends on the interest rate ( i % ), the amount of money deposited, denoted as principal P also called original balance (or initial investment), and the period of time n the money is deposited,

since P : 1 = I : (i · n) then,

Therefore,

and

Solution: Given, P = $20000 , p% = 4.8% and n = 9 months, I = ?

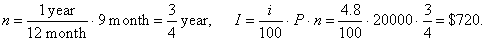
112.

A bank lends a company money for the six months period at a rate of 8% annually.

How much was lent if the company should pay $12,000 of interest?

Solution: Given, I = $12000 , p% = 8% and n = 6 months, P = ?

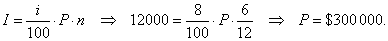
113.

At what an interest rate was borrowed $75,000 for one year if $3,000 to interest is charged?

Solution: Given, P = $75000 , I = $3000 and n = 1 year, i = ?

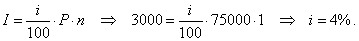
114.

For what period of time should be deposited $200,000 at a 6% interest rate to earn $6,000

of interest?

Solution: Given, P = $200,000 , p% = 6% and I = $6,000, n = ?

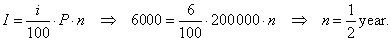
Compound interest

115.

If $10,000 is invested for five years at 6% of the interest rate, find the accumulated or final value and

total interest earned at the end of the period under both, simple and compound interest.

In compound interest calculations, the interest earned in each period is added at the end of a period to the principal of the previous period, to become the principal for the next period.

The compounding periods can be yearly, semiannually, quarterly, or the interest can be compounded more frequently even continuously.

If P is the principal or initial value of investment, A is the accumulated amount or final value of investment and the compound interest rate is i %

then, A = P · r ⁿ, where r = 1 + i, and where

and

Solution: Given, P = $10,000, p% = 6% and n = 5 years, A and I =?

a) Under simple interest, the total interest earned in five years period is

I = i% · P · n => I = 6/100 · 10000 · 5 = $3000,

the accumulated value after five years period is

A = P + I = P (1 + i n) => A = 10000 · (1 + 6/100 · 5) = 10000 · 1.3 = $13000,

so that I = A - P = 13000 - 10000 = $3000.

b) Under compound interest, the accumulated value after five years period is

A = P(1 + i%)ⁿ => A = 10000 · (1 + 0.06)⁵ = 10000 · 1.338225 = $13382.25

therefore, the total interest earned in five years period is

I = A - P = 13382.25 - 10000 = $3382.25.

So, the interest compounding (or interest earned on interest) brings the extra $382.25 in comparison with the simple interest.

116.

After how many years will deposit double at an interest rate of 6%.

Solution:

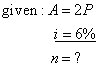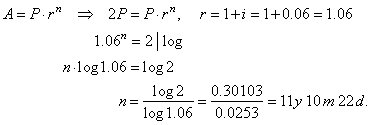117.

At what annual interest has to be deposited $5,000 for four years to grow to $8,000.

Solution:

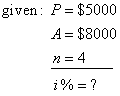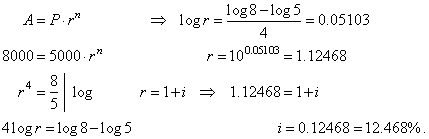Solved problems contents