|
|
|
ALGEBRA
- solved problems
|
|
|
|
|
|
|
|
Radicals
(roots) and/or exponentiation
with fractional (rational) exponent
|
|
| Rationalizing a denominator
|
|
| 75. |
Rationalize given fractions.
|
|
| Solutions: |
 |
| |
 |
|
 |
|
 |
|
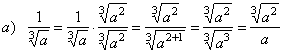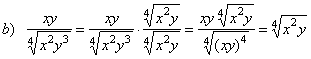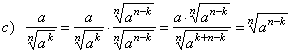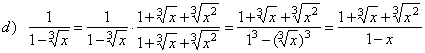since a3 -
b3
=
(a
-
b)
· (a2
+ ab
+ b2) |
|
| Rationalizing a denominator is a method for changing an irrational denominator into a rational one. |
|
| Radicals
and/or fractional
(rational) exponents |
|
| 76. |
Solve given expressions.
|
|
|
|
|
| 77. |
Simplify given expressions.
|
|
|
|
|
|
Algebraic
expressions
|
| Simplifying algebraic
expressions |
|
| 78. |
Simplify algebraic expressions.
|
|
| Solutions: |
|
a)
- 4a3
+
3a2
+
5a3
- 7a2
= (- 4
+
5) · a3
+
(3 - 7)
· a2 = a3 - 4a2, |
|
|
b)
(x2
- x
+
1) ·
(x +
1) =
x3 - x2
+
x
+
x2
- x
+
1 = x3
+
1. |
|
|
| Evaluating algebraic expressions |
|
| 79. |
Evaluate
the expression x2
- 6xy
+
9y2
for x
= 2 and y
= -1.
|
|
| Solution: |
x2
- 6xy
+
9y2
=
22 - 6
· 2
· (- 1)
+
9 ·
(-1)2
= 4 +
12 +
9 = 25. |
|
|
| Expanding
algebraic expression by removing parentheses ( brackets) |
|
| 80. |
Expand given expressions.
|
|
| Solutions: |
|
a)
(a
- b)2 = (a
- b)
· (a
- b) =
a2
- ab
- ab
+
b2
= a2
- 2ab
+
b2, |
|
|
b)
(a - b)
·
(a
+
b) =
a2 - ab
+
ab
- b2 =
a2 -
b2, |
|
|
c)
(x
+
y)
· (x2
- xy
+
y2) =
x3 - x2y
+
xy2
+
x2y
- xy2
+
y3
= x3
+
y3. |
|
|
|
|
The
square of a binomial (or binomial square)
|
|
|
| 81. |
Square given binomials.
|
|
| Solutions: |
|
a)
(a +
b)2 = (a
+ b)
·
(a
+ b) =
a2 +
ab
+ ab
+
b2
= a2
+ 2ab
+
b2, |
|
|
b)
(2x +
3)2 =
(2x)2
+ 2
· (2x) ·
3
+
32
= 4x2 +
12x +
9, |
|
|
c)
(x
- 2y)2 =
x2 +
2 · x
·
(-2y)
+
(-2y)2 =
x2 -
4xy +
4y2. |
|
|
|
| Squaring
trinomial (or trinomial square) |
|
| 82. |
Square given trinomials.
|
|
|
Solutions:
|
|
a) (x2
- 2x
+ 5)2
= (x2)2
+ (2x)2
+ 52
+ 2
·
x2 ·
(-2x)
+ 2
·
x2 ·
5 +
2 ·
(-2x)
·
5
= |
|
|
|
= x4
+ 4x2
+ 25
- 4x3
+ 10x2
- 20x
= x4 - 4x3
+ 14x2
- 20x
+ 25, |
|
|
|
| b) (a3
-
a2b - 3ab2)2
= (a3)2 + (a2b)2
+ (3ab2)2
+ 2a3
(-a2b)
+ 2a3
(-3ab2)
+ 2(-a2b)
(-3ab2)
= |
|
|
= a6
+ a4b2
+ 9a2b4
- 2a5b
- 6a4b2
+ 6a3b3
= a6 - 5a4b2
+ 9a2b4
- 2a5b
+ 6a3b3. |
|
|
| Cube
of a binomial |
|
| 83. |
Cube (rise to third power) given binomials.
|
|
|
Solutions:
|
|
a) (a - b)3
= (a
- b)2
·
(a - b)
= (a2
- 2ab
+
b2)
·
(a - b)
= |
|
|
|
= a3 - 2a2b
+
ab2
- a2b
+
2ab2
- b3
= a3 - 3a2b
+
3ab2
- b3, |
|
|
|
|
|
b) (x - 2)3
= x3 +
3 ·
x2
·
(-2)
+ 3
·
x ·
(-2)2
+
(-2)3
= x3 - 6x2
+
12x
- 8, |
|
|
|
|
|
c) (2x
+ y)3
= (2x)3 +
3 ·
(2x)2
· y
+ 3
·
(2x)
· y2 + y3
= 8x3 +
12x2y
+
6xy2
+ y3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
