|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
|
| Adding
and subtracting same powers |
|
| 60. |
Add or subtract powers.
|
|
| Solutions: |
a)
2a2
+ 5a
- a2
- a
= a2
+ 4a,
b) 3a4
-
7a4
+ a4
=
(3 -
7 + 1) · a4
= -3a4 |
|
| Only the same powers (with same base and the exponent) can be
added or subtracted. |
| We also say
that only like or similar terms can be added. The number that multiply the power is called
coefficient. We add or subtract the same powers by adding or subtracting their
coefficients. |
|
|
| The
rules for powers (or exponents) |
|
|
|
Rules |
|
Examples |
|
|
am
· an
= am
+
n, |
|
a)
a3
· a4 =
a3
+ 4,
b) 24 · 25 = 24 + 5 =
29 = 512, |
|
|
am
¸
an =
am
-
n, |
|
a)
x5
¸
x3
= x5
-
3
= x2,
b) 0.14
¸
0.13 = 0.14
-
3 = 0.1, |
|
|
an
· bn
= (a
· b)n, |
|
a)
24 · 34 = (2
· 3)4
= 64,
b) 45 · 0.85 = (4
· 0.8)5
= 3.25, |
|
|
an
¸
bn
= (a ¸
b)n, |
|
a)
x6
¸
y6
=
(x
¸
y)6,
b) 125 ¸
35 = (12
¸
3)5 =
45, |
|
|
 |
|
 |
|
|
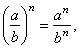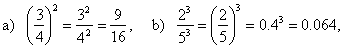(am)n =
am
· n, |
|
a)
(a3)4
= a3
·
4 = a12,
b) (45)3
= 45
·
3 = 415, |
|
|
 |
|
 |
|
|
 |
|
 |
|
|
 |
|
 |
|
|
|
|
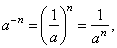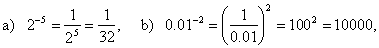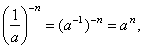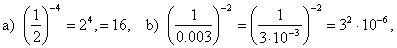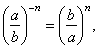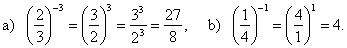| Simplifying an exponential expression |
|
|
| 61. |
Simplify given expressions.
|
|
|
|
|
| Scientific notation |
|
| 62. |
Write in scientific notation and vice versa.
|
|
| Solutions: |
a)
0.0000007054 = 7.054 · 10-7,
b) 5.2 · 10-4
= 0.00052 |
|
| |
c)
4507000000 = 4.507 · 109,
d) 1.04 · 105 = 104000 |
|
|
A
number in scientific notation is written as the product of a
number called coefficient and a power of 10.
|
|
While converting to
scientific notation, the decimal point of the coefficient is
placed behind the first non-zero digit. The sign of the exponent of the power
indicates, how many places the decimal point was moved to the right or to the left.
|
|
|
Quadratic
equation
x2
=
a,
a
>
0
|
|
|
| 63. |
Solve quadratic equations.
|
|
| Solutions: |
a)
x2
= 16 |
|
b) (x
-
5)2
= 49 |
| |
x2
-
42 =
0 |
|
(x
-
5)2
-
72 =
0 |
| |
(x
-
4)
· (x
+
4) =
0 |
|
[(x
-
5) -
7] ·
[(x
-
5) +
7]
=
0 |
| |
x
-
4 =
0 =>
x1
= 4 |
|
(x
-
5) -
7 =
0 =>
x1
= 12 |
| |
x
+
4 =
0 =>
x2
= -
4 |
|
(x
-
5) +
7 =
0 =>
x2
= -2 |
|
| 64. |
Solve quadratic equations.
|
|
|
|
|
|
|
Square
root
|
|
Properties
of square roots
|
|
|
|
|
|
Adding,
subtracting, multiplying and dividing square roots
|
|
| 65. |
Solve given square roots operations.
|
|
|
|
|
|
|
Rationalizing
a denominator
|
|
|
| 66. |
Eliminate radicals from denominators of fractions .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
