|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
|
Properties of the real
numbers
|
|
Properties |
|
Examples |
|
| 1 |
a
+ b
= b
+ a, |
|
5
+ 3 = 3 + 5, |
|
| 2 |
(a
+ b)
+ c
= a
+ (b
+ c), |
|
(2
+ 3) + 5 = 2 + (3 + 5), |
|
| 3 |
a
+ 0
= a, |
|
3
+ 0 = 3, |
|
| 4 |
a
+ (-a)
= 0, |
|
4
+ (-
4)
= 0,
|
|
| 5 |
a
· (b
+ c)
= a
· b
+ a
· c, |
|
2
· (4 + 7) = 2 · 4 + 2 · 7, |
|
| 6 |
a
· b
= b
· a, |
|
6
· 8 = 8
· 6 |
|
| 7 |
a
+ (-b)
= a
-
b, |
|
9
+ (-
4)
= 9
-
4 = 5, |
|
| 8 |
-
(a
+ b)
= -
a
-
b, |
|
-
(3 + 4) = -3
-
4 = -7, |
|
| 9 |
b
-
a
= -
(a
-
b), |
|
5
- 7
= - (7
-
5) = -2, |
|
| 10 |
a
· (-b)
= -
a
· b, |
|
3
· (-
5) = -
3
· 5 =
-15, |
|
| 11 |
(-a)
· (-b)
= a
· b, |
|
(-
3)
· (-
6) = 3
· 6 = 18, |
|
| 12 |
-
(-a)
= a, |
|
-
(-
7) = 7 |
|
| 13 |
a
· 0
= 0, |
|
(-
11)
· 0 = 0,
|
|
| 14 |
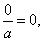 |
|
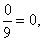 |
|
| 15 |
a
· 1
= 1
· a
= a, |
|
-
5
· 1 = 1
· (-
5) = -
5, |
|
| 16 |
(-1)
· a
= -
a, |
|
(-1)
· 4 = -
4, |
|
| 17 |
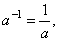 |
|
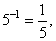 |
|
| 18 |
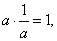 |
|
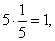 |
|
| 19 |
 |
|
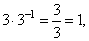 |
|
| 20 |
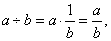 |
|
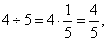 |
|
| 21 |
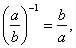 |
|
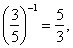 |
|
| 22 |
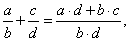 |
|
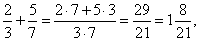 |
|
| 23 |
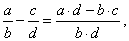 |
|
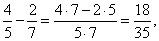 |
|
| 24 |
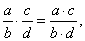 |
|
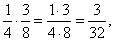 |
|
| 25 |
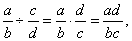 |
|
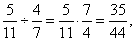 |
|
| 26 |
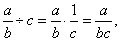 |
|
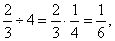 |
|
| 27 |
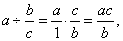 |
|
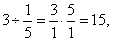 |
|
| 28 |
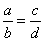 |
if |
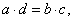 |
|
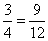 |
since |
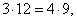 |
|
| 29 |
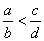 |
if |
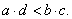 |
|
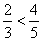 |
since |
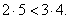 |
|
|
|
|
|
|
|
| Properties of
exponents
|
|
Properties
|
|
Examples |
| 1) |
a
· a
· · · a
= an,
n factors
(exponent), a
-base, |
|
a3
= a · a
· a,
24 =
2 · 2 ·
2 ·
2
= 16, |
| 2) |
a
= a1,
or a1
=
a, |
|
2 = 21,
(-3)1
= -3, |
| 3) |
a0
= 1,
an ¸
an
= 1, |
|
23
¸ 23
= 23 -
3 =
20
= 1,
(ab3)0
= 1, |
| 4) |
1n
=
1, |
|
15
= 1, (-1)5
= -1, |
| 5) |
(-
a)2n
= a2n,
2n
-even exponents, |
|
(-
5)4 = 54
= 625, |
| 6) |
(-
a)2n
-1
= - a2n
-1,
2n-1
-odd exponents, |
|
(-
2)3 = -
23
=
- 8, |
| 7) |
(-1)2n
= 1, |
|
(-1)6
= 1, |
| 8) |
(-1)2n
-1
= -1, |
|
(-1)7
= -1. |
|
|
| The
rules for powers or exponents
|
|
Rules
|
|
Examples |
| 1) |
am
· an
= am
+
n, |
|
a)
a3
· a4 =
a3
+ 4,
b) 24
· 25 = 24 + 5 = 29
= 512, |
| 2) |
am
¸
an
=
am
-
n, |
|
a)
x5
¸
x3
= x5
-
3
= x2,
b) 0.14
¸
0.13 = 0.14
-
3 = 0.1, |
| 3) |
an
· bn
= (a
· b)n, |
|
a)
24
· 34 = (2
· 3)4
= 64,
b) 45
· 0.85 = (4
· 0.8)5
= 3.25, |
| 4) |
an
¸
bn
= (a ¸
b)n, |
|
a)
x6
¸
y6
= (x
¸
y)6,
b) 125 ¸
35 = (12
¸
3)5 =
45, |
| 5) |
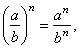 |
|
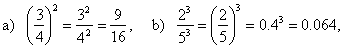 |
| 6) |
(am)n
=
am
· n, |
|
a)
(a3)4
= a3
·
4 = a12,
b) (45)3
= 45
·
3 = 415, |
| 7) |
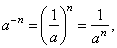 |
|
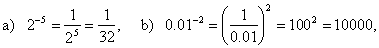 |
| 8) |
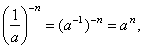 |
|
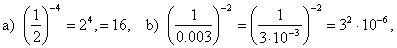 |
| 9) |
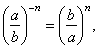 |
|
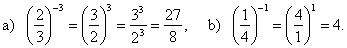 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|