|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
 Sets
Sets |
| 1. |
If
S
is the set { 1, 2, 3 } then power set of S,
|
|
| Solution:
P (S)
= { {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. |
|
| 2. |
Assuming
the set of natural numbers N
is the universal set given are sets,
|
|
|
A = {
x Î
N
|
x <
5
},
B
= {
x Î
N
|
3
≤ x <
8 }
and
C = {
x Î
N
|
x =
2n
− 1,
n
Î N
}. |
|
Find: a) A
∩ B,
b) A
U B,
c)
A
− B,
d)
B
− A
and e)
C'. |
| Solution:
As A
= {
x Î
N
|
x <
5
} =
{ 1, 2, 3, 4 }, |
|
B = {
x Î
N
|
3
≤ x <
8 }
=
{ 3, 4, 5, 6, 7 } |
|
and C
= {
x Î
N
|
x =
2n
− 1,
n
Î
N
}
= {
1, 3, 5, 7, . . . } |
|
then a) A
∩ B
=
{ 3, 4 },
b) A
U B
=
{ 1, 2, 3, 4, 5, 6,
7 }, |
|
c)
A
− B
=
{ 1, 2 },
d)
B
− A
=
{ 5, 6, 7 } |
| and
e) C'
= {
x Î
N
|
x =
2n
} = {
2, 4, 6, 8, . . . }. |
|
| 3. |
If
given set {1, 2, 3, 4, 5, 6, 7} then one of its
possible partitions is
|
|
| Solution:
{ {1, 3, 7}, {2}, {4, 5}, {6} }. |
|
 Relations
Relations |
|
| 4. |
Given is
set S
= {1, 3, 5, 7, 9} and relations on S:
|
|
|
R1 = {(1, 3), (3, 5), (5, 1), (3, 7), (7, 9), (9, 1)}, |
|
R2 = {(1, 1), (3, 3), (5, 5), (7, 7), (9, 1)}, |
|
R3 = {(1, 5), (3, 7), (7, 1), (9, 5), (1, 1)}, |
|
R4 = {S
× S}. |
| Which of these relations is function from
S
to S ? |
| Solution:
A binary relation R, a subset of the Cartesian product A
×
B, is said to be a function from
A to
B if for
each x Î
A there is exactly one
y
Î
B, such that the pair
(x,
y) is in subset R. The set A is called the domain of the function, and the set
B is called the codomain of the function. |
|
Thus, R2 = {(1, 1), (3, 3), (5, 5), (7, 7), (9, 1)} is the function from
S
to S. |
|
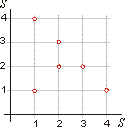
| 5. |
Supplement the relation
R
= {(1, 1), (2, 2), (3, 2), (4, 1)}, defined on the set
S
= {1, 2, 3, 4}, with
|
|
| minimal number of elements of the product set
S
×
S
such that the relation becomes symmetric. |
| Solution:
The given relation should be supplemented with pairs |
| (1, 4)
and (2, 3). |
| The relation
R
= {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (4, 1)} is symmetric (in |
| relation to the main diagonal). |
|
 |
|
|
|
|
 Binary
numbers
Binary
numbers |
|
| 6. |
Convert given binary
number to its decimal
equivalent by writing it in
a place-value notation:
|
|
| Solution:
1 0 1 1 1 0 1 =
1 · 26 + 0
· 25
+ 1 · 24 + 1 · 23
+ 1 · 22 + 0 ·
21
+ 1 · 20 = |
|
= 64 + 0
+ 16 + 8
+ 4 +
0 + 1
= 93. |
|
| 7. |
Convert given decimal
number to its binary equivalent:
|
|
| Solution: (113)10
=> ( 1
1 1 1 0 0 0 1
)2 |
| To convert a decimal number to its
binary equivalent |
| divide given decimal and each successive
quotient by |
| 2 noting remainders from right to left, i.e., form
the |
| lowest place value to the higher.
The remainders can |
| only be 0 and 1 since divisions are by 2. The
division |
| ends by the quotient
zero |
|
| 113 |
÷ |
2 |
= |
1
1 1 1 0 0 0 1 |
| 56 |
|
|
|
<===== |
| 28 |
|
| 14 |
| 7 |
| 3 |
| 1 |
| 0 |
|
|
| Binary
operations |
|
| 8. |
Add given binary
numbers:
|
|
| Solution:
The
binary system works under the same principles as the decimal
system as show basic rules for binary addition. |
| (1) |
|
|
|
0 |
+ |
0 |
= |
|
0 |
|
|
| (2) |
|
|
|
0 |
+ |
1 |
= |
|
1 |
| (3) |
|
|
|
1 |
+ |
0 |
= |
|
1 |
| (4) |
|
|
|
1 |
+ |
1 |
= |
1 |
0 |
(with a carry of
1) |
| (5) |
|
1 |
+ |
1 |
+ |
1 |
= |
1 |
1 |
(with a carry of
1) |
|
or |
| (1) |
(2)
and (3) |
(4) |
(5) |
|
|
|
1 |
|
0 |
1 |
1 |
1 |
| + 0 |
+
0 |
+
1 |
+
1 |
|
0 |
1 |
10 |
11 |
|
|
|
When adding two multiple digits numbers a carry
has to be added to the
next higher place value digit.
|
|
1 |
1 |
carry |
|
|
1 |
1 |
0 |
1 |
0 |
|
=> |
26 |
|
+ |
1 |
1 |
1 |
0 |
0 |
|
=> |
+ 28 |
|
1 |
1 |
0 |
1 |
1 |
0 |
sum |
54 |
|
|
|
| The
method of subtraction by adding complement of the subtrahend
applied to decimals |
| 9. |
Calculate the
difference D = A − B,
where A = 423 minuend (M) and B = 79 subtrahend
(S).
|
|
| Solution:
423 − 79 =
423 + (100 − 79 −
100) = 423 + 21− 100 = 344,
by using this method we can avoid |
|
subtraction of larger
from smaller digits thus, when calculating the complement of the
subtrahend (CS) we |
| write 100 − 79 =
99 + 1 − 79 = 21. |
|
| The
method of subtraction by adding complement of the subtrahend
applied to binary numbers |
| 10. |
Calculate the
difference D = A − B,
where A = 101000(40) and B = 10111(23).
|
|
| Solution: The
calculation of the complement, |
| 1000000 −
10111 = 111111 + 1 − 10111 =
101000 + 1 = 101001 (CS) |
| then,
101000 −
10111 = 101000
+ (1000000 −10111−1000000) =
101000 + 101001 −
1000000 = 10001 |
| Proof:
the binary complement of 10111(23) is 101001(41)
since 10111(23) + 101001(41) =
1000000(64) = 26. |
| Computers
form the complement in two steps, first invert all bits of the
number by changing all of the ones to zeroes and all of the
zeroes to ones (which is called one's complement). Then, add 1
to the result, thus forming, so called the two's complement of
the given number. |
| Since
computers use fixed-length fields, the complement from above
example is shown in 8 bits: |
| 0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
(23) |
| 1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1's
complement |
|
+ |
1 |
|
|
| 1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
2's
complement |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
(23) |
| + |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
(133)
CS |
|
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
=
256 = 28
|
|
|
| Then
by adding the minuend and the complement of the subtrahend
obtained is the difference. |
| Notice that the
leading 1 (overflow), that occurs in the
highest-order bit of the result, equals the
corresponding place value 28
which
must be subtracted from the result as the above
algorithm shows. |
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
Minuend |
| + |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
CS |
|
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Result |
|
|
| Binary
multiplication is the same as repeated binary addition, and
binary division is the repeated process of subtraction, just as
in decimal division. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|