|
| Trigonometry |
|
|
|
|
|
Graphs of
Trigonometric Functions |
|
The
Graph of the Cosine Function f
(x) = cos
x |
Properties of the
cosine function |
|
Domain and range |
|
Zeros of the function |
|
Extremes, maximum and
minimum of the cosine function |
|
Parity and periodicity
of the cosine function |
|
Behavior of the cosine
function |
|
|
|
|
|
|
|
|
Graphs of
trigonometric functions |
|
Visual presentation of changes and behavior of each trigonometric function shows us its graph in the coordinate plane
xOy.
|
| A graph of a function is formed by points
P(x, f (x)), where the abscissas
x
belong to the domain and the calculated values of the function f
(x)
as the ordinates, which are the corresponding values from the range.
|
|
|
The graph of the cosine function f
(x) = cos
x |
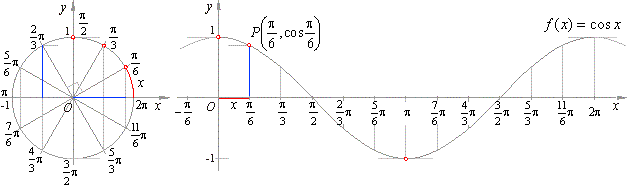
| To draw the graph of the cosine function divide the unit circle and
x-axis of a Cartesian coordinate system the
same way
as when drawing the sine function. |
| The abscissas of the ending points of arcs
x, of the unit
circle, are now the ordinates of the corresponding points P(x,
cos x) of the graph, as shown in
the figure below. |
 |
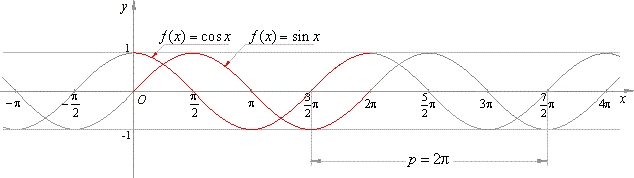
| Since
cos x
= sin (x + p/2)
that
is, the cosine of an arc x equals the sine of the same arc increased by
p/ 2. |
|
| Therefore, the graph of the
cosine function correspond to the graph of the sine function translated in the negative direction
of the x-axis by
p/ 2. |
| Thus
for example, cos
p/6
= sin (p/6 +
p/ 2)
= sin 2p/3
as shows the above graph. |
 |
|
| Properties of the
cosine function |
| - Domain,
x Î
R. |
| - Range,
-1
<
y <
1. |
| - Zeros of the
function,
x
= p/2 +
kp,
k Î
Z. |
| -
Abscissas
of maximums,
x
= k · 2p,
k
Î
Z
and minimums
x
= (2 k + 1) · p,
k
Î
Z. |
| -
Parity
and periodicity, the cosine
is even function since f
(-x) =
cos(-x) = cos
x = f (x). |
|
The identity cos
(x + k · 2p) = cos
x, k Î
Z shows that the cosine is periodic
function with the period P
= 2p. |
| |
|
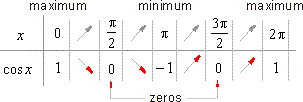
| Behavior of the cosine function |
| The table shows behavior of the cosine function while the arc
x
of the unit circle increases passing through all
the values from the period. |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
