|
| Trigonometry |
|
|
|
|
Sum to product and
product to sum formulas or identities |
|
Sum to product formulas
for the tangent and the cotangent functions |
|
The product to sum
formulas for the sine and cosine functions |
|
Trigonometric identities,
examples |
|
|
|
|
|
|
| Sum to product and
product to sum formulas or identities |
|
| Sum to product formulas
for the tangent and the cotangent functions |
| From the definition of the function tangent, |
 |
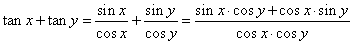| or |
 |
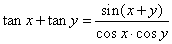and |
 |
|
|
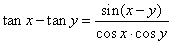| and
for the function cotangent |
 |
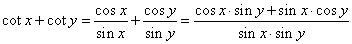| or |
 |
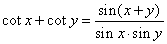and |
 |
|
|
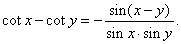| Using
the same method, |
|
 |
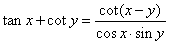and |
 |
|
|
|
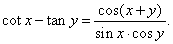| The product to sum
formulas for the sine and cosine functions |
| By adding and subtracting addition formulas derived are following product
to sum formulas, |
| |
 |
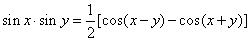and |
 |
|
|
| |
 |
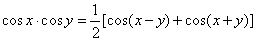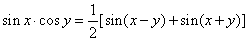and |
 |
|
|
|
|
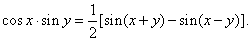| Trigonometric identities,
examples |
|
| Example:
Verify the identity |
 |
|
|
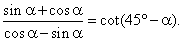Solution:
We divide the numerator and
denominator on the left side by sin
a
and to the right side we use the cotangent formula for the
difference of two angles, thus
|
 |
 |
|
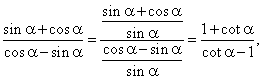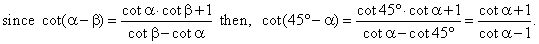| Example:
Express tan
3x in terms of tan
x. |
| Solution:
Using the sum formula and the double angle formula for the
tangent function, |
 |
|
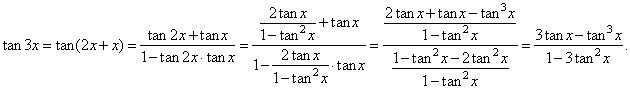| Example:
Prove the identity |
 |
|
|
|
|
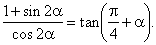| Example:
Prove the identity |
 |
|
|
|
|
|
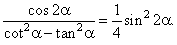Example:
If tan
a
= 3/4, find tan
a/2.
|
| Solution:
Use formula |
 |
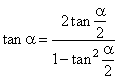to express tan
a/2
in terms of tan
a. |
|
 |
|
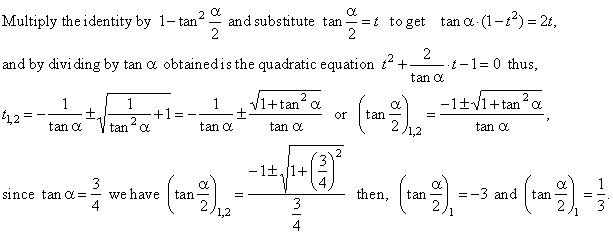| Example:
Prove the identity |
 |
|
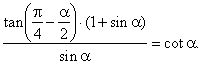| Solution:
Substitute |
 |
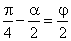then |
|
 |
|
|
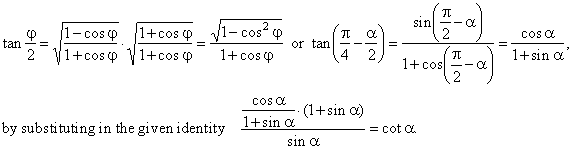Example:
Express the given
difference sin
61° -
sin 59° as a product.
|
| Solution:
Since |
 |
|
 |
|
|
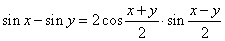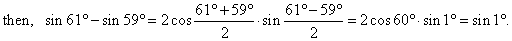Example:
Prove the identity sin a
+ sin (a
+ 120°) +
sin (a
+ 240°)
= 0.
|
|
Solution:
Applying the sum formula to
the last two terms on the left side of the identity we get,
|
 |
|
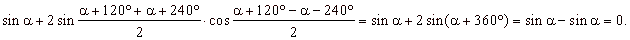| Example:
Prove the identity |
 |
|
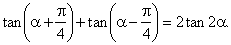| Solution:
Using the formula for the sum of the tangent |
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
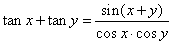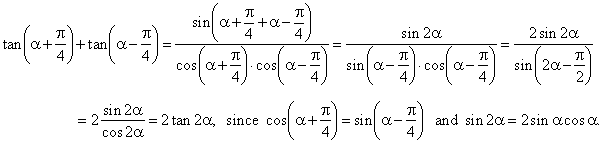| Pre-calculus contents
F |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
