|
|
|
|
Rational Expressions
|
 Multiplication and division of rational
expressions
Multiplication and division of rational
expressions
|
 Solving complex rational expressions
Solving complex rational expressions
|
|
|
|
|
|
|
| Multiplication and division of rational
expressions
|
| Use
the formulas for the multiplication
and the division of fractions. |
| |
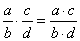 |
and |
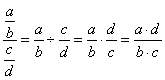 |
|
|
| Notice
the two special cases of which should be aware of: |
| |
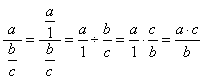 |
and |
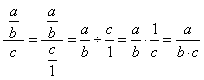 |
|
|
|
| Examples:
Perform the indicated
operations and reduce the answer to lowest terms. |
|
|
| Note,
since each second line should be subtracted, the sign of each term is reversed. |
|
| Solving complex rational expressions
|
| A complex or compound rational expression has fractional expressions in its numerator, denominator or both. |
| To simplify complex fractions, change the complex fraction into a division problem, i.e., divide the numerator by the denominator. |
| Examples:
Simplify complex
fractions. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents A
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |