|
|
|
|
Absolute value
equations, quadratic
equations and functions |
 Solving quadratic
equations with absolute value
Solving quadratic
equations with absolute value |
 Graphing absolute value
functions or equations, examples
Graphing absolute value
functions or equations, examples |
|
|
|
|
|
|
| Quadratic
equations with absolute value |
| Graphical
interpretation of the
definition of the
absolute value of a function y =
f (x) will help us solve
an equation with absolute value. |
| The
definition for the absolute value of a function is given by |
|
|
| Thus,
for
values of x
for which f (x)
is nonnegative ( >
0 ), the graph of | f
(x)| is the
same as that of f
(x).
|
| For values of
x
for which f (x)
is negative ( <
0 ), the graph of | f
(x)
| is a reflection of
the graph of f (x)
on the x-axis. That
is, the
graph of y = -
f
(x) is obtained by reflecting the graph
of y = f
(x)
across the x-axis. |
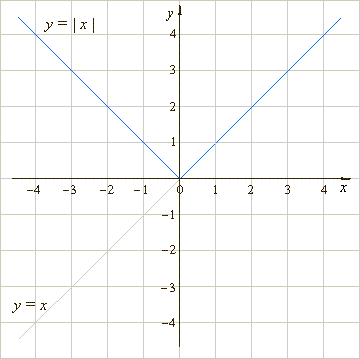
| Hence,
the graph of the absolute value of
the function
y =
x,
i.e.,
| x | is |
 |
|
| Example:
Solve the absolute value
equation
| x2
-
3 | =
-
x + 3. |
| Solution:
Using the definition of the
absolute value of a function we can write, |
| if
x2
-
3 > 0
then |
x2 -
3 | =
x2 -
3, |
| and
given equation x2
-
3 =
-
x + 3
or |
|
x2
+ x -
6 =
0.
By
factoring the equation, |
|
x2 +
3x
-
2
x -
6 =
[x(x + 3) -
2(x + 3)] |
|
x2
+ x -
6 =
(x + 3)(x -
2) =
0 |
| so,
x
+ 3 =
0,
x1
= -
3
and x
-
2 =
0,
x2
= 2. |
| If
x2
-
3 < 0
then |
x2 -
3 | =
-
(x2
-
3), |
| and
given equation -
(
x2 -
3) =
-
x + 3
or |
| -
x2
+
x =
x(-
x + 1) =
0 |
| so,
x3
= 0
and -
x + 1 =
0,
x4
= 1. |
|
 |
|
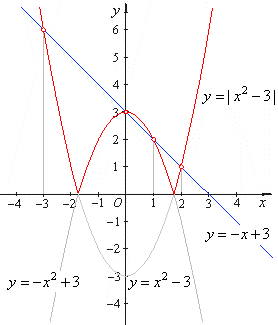
| Therefore,
the solutions of the given equation, x1
= -
3, x2
= 2,
x3
= 0
and x4
= 1 are the abscissas of the
intersection points of, y = |
x2 -
3 | and y = -
x + 3
functions, as is shown in the above figure. |
|
| Example:
Solve the absolute value
equation
| 2x2
-
x -
3 | =
-
x + 5. |
| Solution:
Using the definition of the
absolute value of a function we can write, |
| if
2x2
-
x -
3 > 0 |
| then
|
2
x2
-
x -
3 | =
2
x2
-
x -
3, |
| and
given equation 2
x2
-
x -
3 =
-
x + 5 |
|
or 2x2
=
8,
x2
=
4, |
| so,
x1,2
= ±
2,
x1
= -
2
and x2
= 2. |
| if
2
x2
-
x -
3 < 0 |
| then
|
2x2
-
x -
3 | =
-
(2x2
-
x -
3), |
| and
given equation -
(2
x2
-
x -
3) =
-
x + 5, |
|
-
2x2
+
2x
-
2
= 0
or x2
-
x + 1
= 0, |
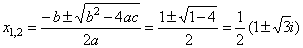 |
| thus,
there are no real solutions in this case. |
|
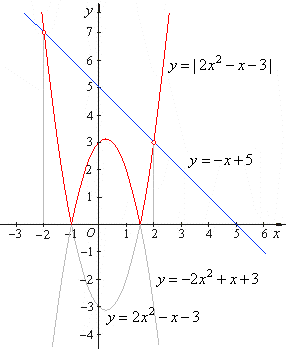 |
|
|
Therefore,
the solutions of the given equation, x1
= -
2 and x2
= 2 are the abscissas of the
intersection points of, y = |
2
x2
-
x -
3 | and y = -
x + 5
functions, as is shown in the above figure. |
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents B |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |