|
|
|
|
Quadratic
inequalities
|
 Solving
quadratic inequalities
Solving
quadratic inequalities |
 Graphic solution of
quadratic inequalities
Graphic solution of
quadratic inequalities |
|
|
|
|
|
|
|
Quadratic
inequalities
|
| To solve a quadratic inequality we can examine the sign of the
equivalent quadratic function. |
| The
x-intercepts
or roots are the points where a quadratic function changes the sign. The
x-intercepts determine
the three intervals on the x-axis in which the function is above or
under the x-axis, that is, where the function is positive or negative. |
|
| Graphic solution of
quadratic inequalities |
| Example:
Solve the inequality
-
x2
+ 2x
+
3 ≤
0. |
| Solution:
Solve the quadratic
equation ax2
+ bx
+
c
=
0
to get the boundary points. |
| The zeroes
or roots of equivalent function (see the graph
below) are the endpoints of the intervals and are included in the solution. |
|
The turning point V(x0,
y0), |
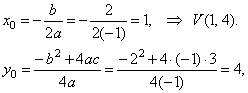 |
|
The roots, -
x2
+ 2x
+
3 =
0 |
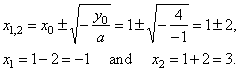 |
|
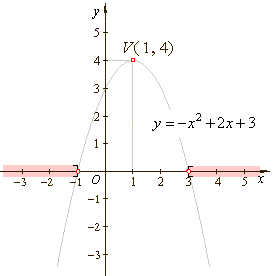 |
| Solution: |
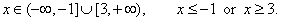 |
|
|
|
| Example:
Solve the inequality |
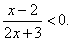 |
|
|
| Solution:
A fraction is negative if
the numerator and the denominator have opposite signs. |
| Thus,
we have to solve the two systems of inequalities |
| a) x -
2 <
0 and b)
x -
2 >
0 |
|
2x +
3 >
0 2x +
3 <
0 |
|
|
|
x <
2 x >
2 |
|
x >
-3/2. x <
-3/2 |
| Where b) represents the system
of the contradictory inequalities. |
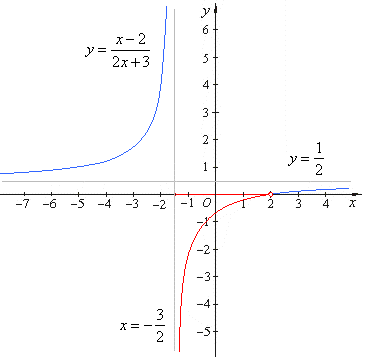
| The
red colored part of the graph of the
corresponding equilateral or rectangular
hyperbola shows the interval (region) where the
function's values are negative. |
| Thus,
the solution is -3/2
<
x <
2. |
|
 |
|
| Or,
we can transform the given fraction to the quadratic inequality
by multiplying it by (2x
+
3)2. |
| So,
obtained is |
| (x -
2)(2x
+
3)
<
0
or
2x2
-
x
-
6 <
0. |
| The
roots of the corresponding function, |
| x -
2 = 0,
x1
= 2
and 2x
+
3 = 0,
x2
= -3/2 |
| Therefore,
the solution is |
| -3/2
<
x <
2. |
| The
right figure shows that the graph of the
function is negative in this interval. |
|
|
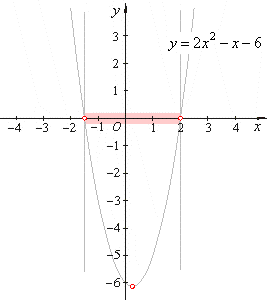 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents B |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |