| Vieta's
formulas |
| Suppose,
r1, r2, r3,
· · · ,
rn,
are roots of a polynomial f
(x)
of degree n
(counting multiplicities) with
leading coefficient an
= 1,
that is, |
| f
(x)
= xn
+ an-1xn-1
+ an-2xn-2
+
.
. . +
a2x2
+ a1x
+ a0 |
|
then we can write f
(x)
= (x
- r1)(x
- r2)(x
- r3)
· · · (x
- rn).
|
| By
expanding the above expression and collecting like terms, and
after comparing corresponding coefficients of
both expressions, we get |
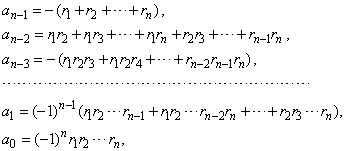 |
| Vieta's
formulas that show coefficients and roots relations. |
| Note
that the coefficients of a polynomial are expressed as the sum
of corresponding combinations of
roots. |
| Let
write coefficients of the quadratic polynomial by roots |
|
f (x)
= x2
+ a1x
+ a0
= (x
- r1)(x
- r2)
=
x2
-
(r1
+ r2)x
+ r1r2, |
| the
cubic polynomial |
|
f (x)
= x3
+
a2x2
+ a1x
+ a0
= (x
- r1)(x
- r2)(x
- r3)
or |
|
f (x) =
x3
-
(r1
+ r2
+ r3)x2
+ (r1r2
+ r1r3
+ r2r3)x
-
r1r2r3, |
| and
the quartic polynomial |
|
f (x)
= x4
+
a3x3
+
a2x2
+ a1x
+ a0
= (x
- r1)(x
- r2)(x
- r3)(x
- r4)
or |
|
f (x) =
x4
-
(r1
+ r2
+ r3
+ r4)x3
+ (r1r2
+ r1r3
+ r1r4
+ r2r3
+ r2r4
+ r3r4)x2
- |
|
-
(r1r2r3
+ r1r2r4
+ r1r3r4
+ r2r3r4)x
+ r1r2r3r4. |
|
| Example:
Write the cubic
polynomial whose roots are r1
= 1 and r2,3
= 1 ±
i, assuming its
leading coefficient a3
= 1. Find its source function
and draw their graphs. |
| Solution:
Let write the cubic polynomial by roots |
|
f (x)
= x3
-
(r1
+ r2
+ r3)x2
+ (r1r2
+ r1r3
+ r2r3)x
-
r1r2r3, |
| and
calculate coefficients |
|
a2
=
-
(r1
+ r2
+ r3)
=
-
[1
+ (1 + i)
+ (1 -
i)]
=
-
3, |
|
a1
=
r1r2
+ r1r3
+ r2r3
=
1 ·
(1 + i)
+ 1
·
(1 -
i)
+ (1 + i)
·
(1 -
i)
=
4, |
|
a0
=
-
r1r2r3
=
-
1 ·
(1 + i)
·
(1 -
i)
=
-
2, |
| therefore
f (x)
= x3
-
3x2
+ 4x
-
2
or f
(x)
= (x
-
1)[x
- (1 + i)][x
- (1
-
i)] |
| To
find the source form, fs(x)
=
a3x3
+ a1x
of the general cubic polynomial
we should calculate |
| coordinates
of translations x0
and y0, |
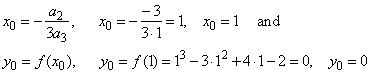 |
|
and plug into y
+ y0
= a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0)
+
a0 |
|
thus,
y
= (x
+
1)3
- 3(x
+ 1)2
+ 4(x
+ 1)
- 2
= x3
+ x
or fs(x)
= x3
+ x. |
| Alternatively,
coefficients of the source polynomial can be calculated like
coefficients of the Taylor polynomial |
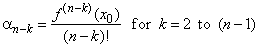 |
| since,
an
= an,
an
-1
= 0 and a0
= f
(x0),
and where f (n
-
k)
(x0)
denotes (n
-
k)-th derivative at
x0. |
| Hence,
f (x)
= x3
- 3x2
+ 4x
- 2, f '(x)
= 3x2
- 6x
+ 4
and f '(x0)
or f '(1)
= 3x2
- 6x
+ 4
= 1
then |
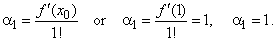 |
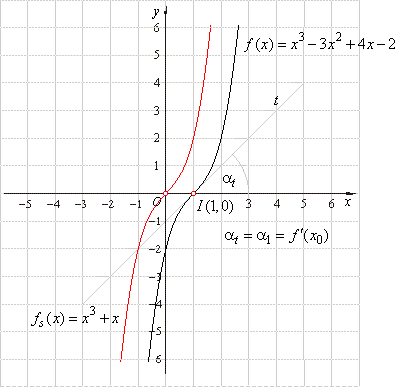 |
| Therefore,
the given cubic polynomial is translated only in the direction
of the x-axis
by x0
= 1, as shows the above
picture. Note that the point of inflection of a cubic polynomial
I (x0,
y0), since f
'' (x0) = 0. |
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
E |
|
 |
|