|
|
There
are three types of the cubic functions - the classification
criteria diagram |
|
The graphs
of the source cubic functions |
|
|
|
|
|
|
|
| The
graphs
of the source cubic functions |
| There are three types
(shapes) of cubic
functions whose graphs of the source functions are shown in the figure below: |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or y
-
y0
= a3(x
-
x0)3,
-
a22
+ 3a3a1
= 0 or a1
= 0. |
|
| therefore,
its source function y
=
a3x3,
and the tangent line through the point of
inflection is horizontal. |
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1>
0 |
|
| whose
slope of the tangent line through the point of inflection is
positive and equals a1. |
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1<
0 |
|
| whose
slope of the tangent line through the point of inflection is
negative and is equal a1. |
| The
graph of its source function has three zeros or roots at |
 |
|
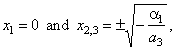| and two turning
points at |
 |
|
| |
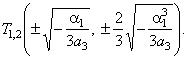| The
graphs
of the source cubic functions - the classification criteria
diagram |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
E |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
