|
|
| Polynomial and/or Polynomial
Functions and Equations |
 Cubic functions
Cubic functions |
|
Transformation of the cubic
polynomial from the general to source form and vice versa |
|
Coordinates
of the point of inflection coincide with the coordinates of
translations |
|
The
source cubic functions are odd functions |
|
|
|
|
|
|
|
| Cubic
function
y
=
a3x3
+
a2x2
+
a1x + a0 |
| Transformation of the
cubic polynomial from the general to source form and vice versa |
| Applying
the same method we can examine the third degree polynomial
called cubic function. |
| 1)
Calculate the
coordinates of translations |
| substitute
n
= 3
in |
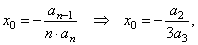 |
|
|
| and |
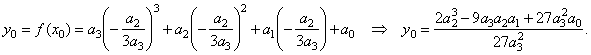 |
|
| 2)
To
get the source cubic function we should plug the coordinates
of translations (with changed signs) |
|
into the general form
of the cubic,
i.e., |
| y
+ y0
= a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0)
+
a0, |
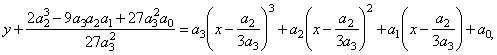 |
| after
expanding and reducing obtained is |
| |
 |
the source
cubic function. |
|
| 3)
Inversely, by plugging the coordinates of translations into the source
cubic |
|
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
|
|
|
after
expanding and reducing we obtain |
|
y
=
a3x3
+ a2x2
+ a1x
+ a0
the cubic function
in the general form. |
| Thus,
y
=
a3x3
+ a2x2
+ a1x
+ a0
or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
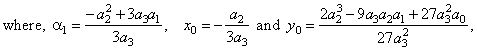 |
| by
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tan at
. |
|
|
|
| Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I
(x0,
y0).
|
| The
source cubic functions are
odd functions. |
| Graphs of odd functions are
symmetric about the origin that is, such functions change
the sign but not absolute value when the sign of the independent variable is
changed, so that f
(x)
=
-
f (-x). |
| Therefore,
since f (x)
= a3x3
+
a1x
then -
f
(-x)
= -[a3(-x)3
+
a1(-x)]
= a3x3
+
a1x
=
f (x). |
| That
is, change of the sign of the independent variable of a function
reflects the graph of the function about the y-axis,
while change of the sign of a function reflects the graph of the
function about the x-axis. |
| The
graphs of
the translated cubic functions are symmetric about its
point of inflection. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
E |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |